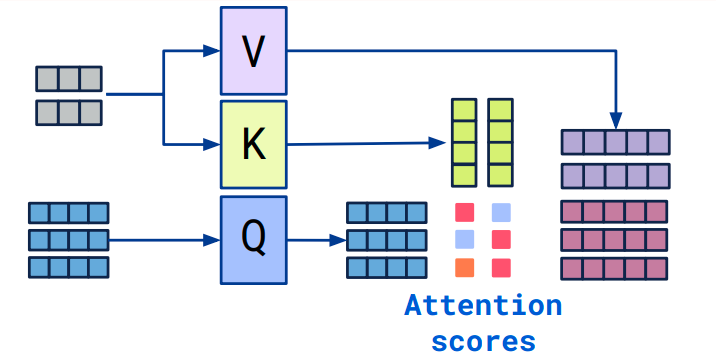
Self-Attention 是 Transformer 中最核心的思想。我们在阅读 Transformer 论文的过程中,最难理解的可能就是自注意力机制实现的过程和繁杂的公式。
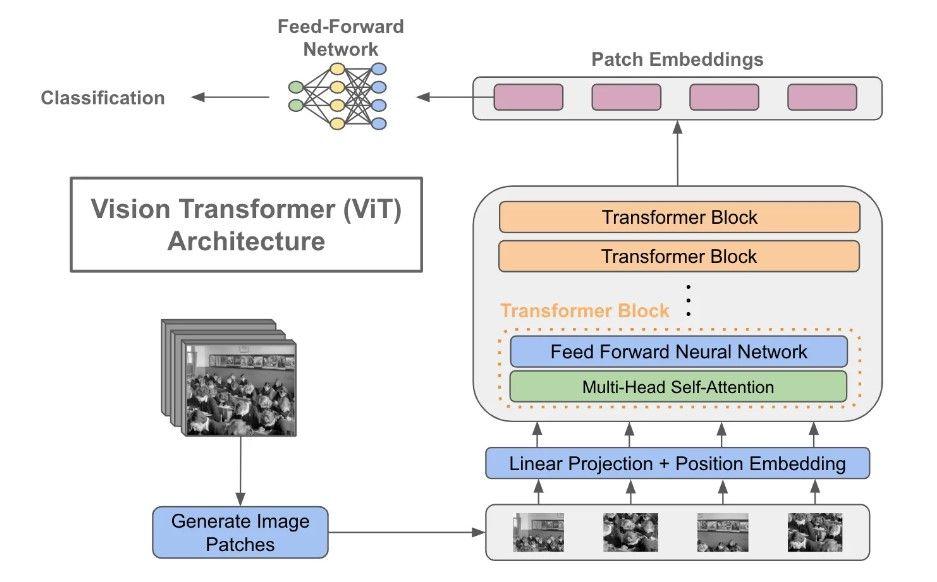
Self-Attention 是 Transformer 中最核心的思想。我们在阅读 Transformer 论文的过程中,最难理解的可能就是自注意力机制实现的过程和繁杂的公式。本文在 Illustrated: Self-Attention 这篇文章的基础上,加上了自己对 Self-Attention 的理解,力求通俗易懂。希望大家批评指正。
1. Self-Attention 是什么?
我们再来讲解一个重要的概念,即 query、key 和 value。这三个词翻译成中文就是查询、键、值,看到这中文的意思,还是迷迷糊糊的。我们来举个例子:小明想在 b 站搜索深度学习,他把深度学习四个字输入到搜索栏,按下搜索键。搜索引擎就会将他的查询 query 映射到数据库中相关的标签 key,如吴恩达、神经网络等等,然后向小明展示最匹配的结果 value。
最后我们来说说 Self-Attention。和 Attention 类似,他们都是一种注意力机制。不同的是 Attention 是 source 对 target,输入的 source 和输出的 target 内容不同。例如英译中,输入英文,输出中文。而 Self-Attention 是 source 对 source,是 source 内部元素之间或者 target 内部元素之间发生的 Attention 机制,也可以理解为 Target=Source 这种特殊情况下的注意力机制。
下面我们通过一个简单的例子,来了解 Self-Attention 的计算步骤。
2. 计算步骤
2.1 定义 input
在进行 Self - Attention 之前,我们首先定义 3 个 1×4 的 input。 pytorch 代码如下:
1 | import torch |

2.2 初始化权重
每个 input 和三个权重矩阵分别相乘会得到三个新的矩阵,分别是 key(橙色),query(红色),value(紫色)。我们已经令 input 的 shape 为 1×4,key、query、value 的 shape 为 1×3,因此可以推出与 input 相乘的权重矩阵的 shape 为 4×3。 代码如下:
这三个不同的权重矩阵($W_Q、W_K、W_V$)是通过神经网络模型的训练过程自动学习而来的。在自注意力机制中,这些矩阵是模型参数的一部分,它们的初值通常是随机初始化的。然后,通过训练数据和反向传播算法,模型会逐渐调整这些矩阵的值,以最小化预测误差(比如分类任务中的交叉熵损失)。
1 | w_key = [ |
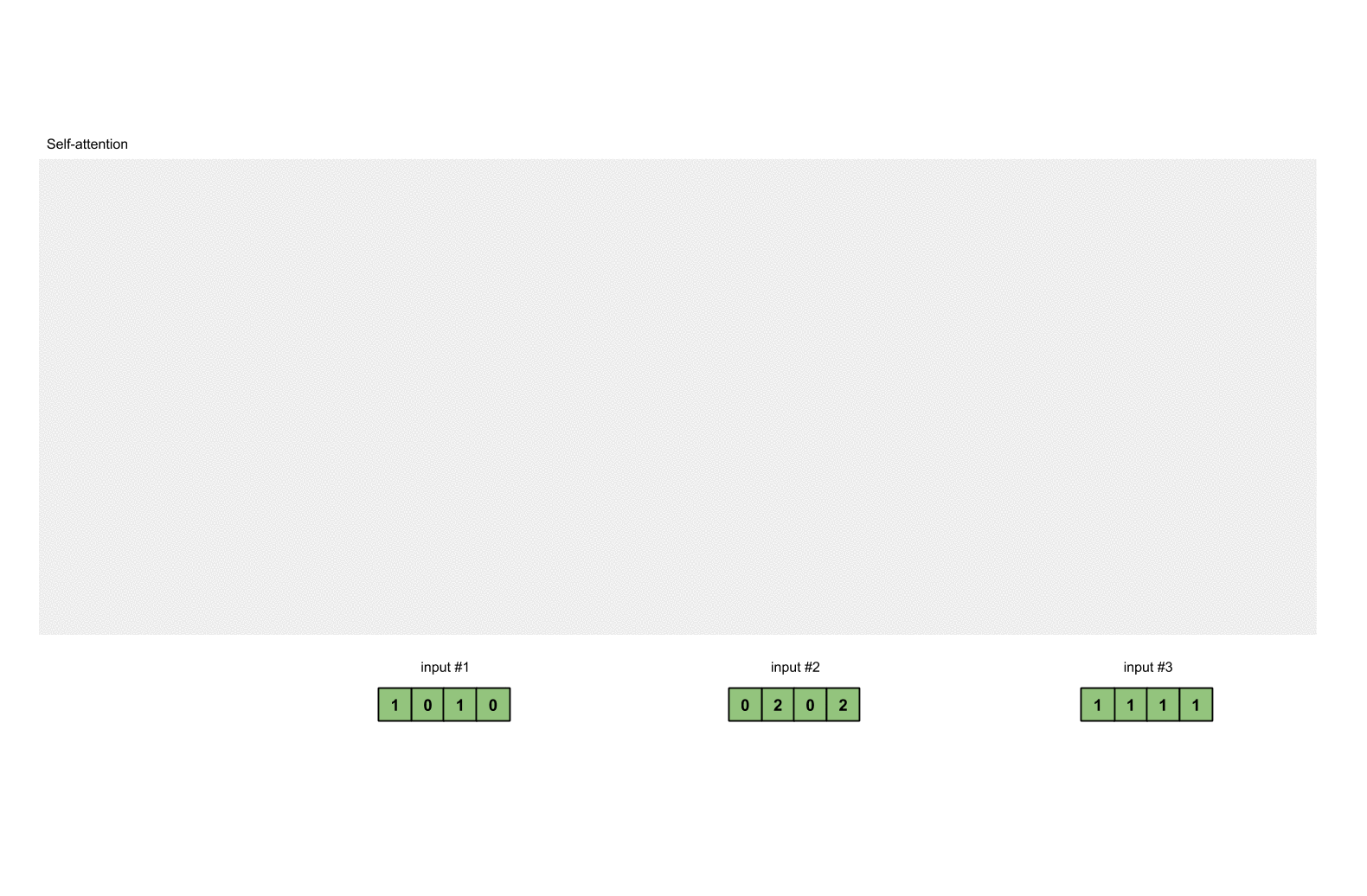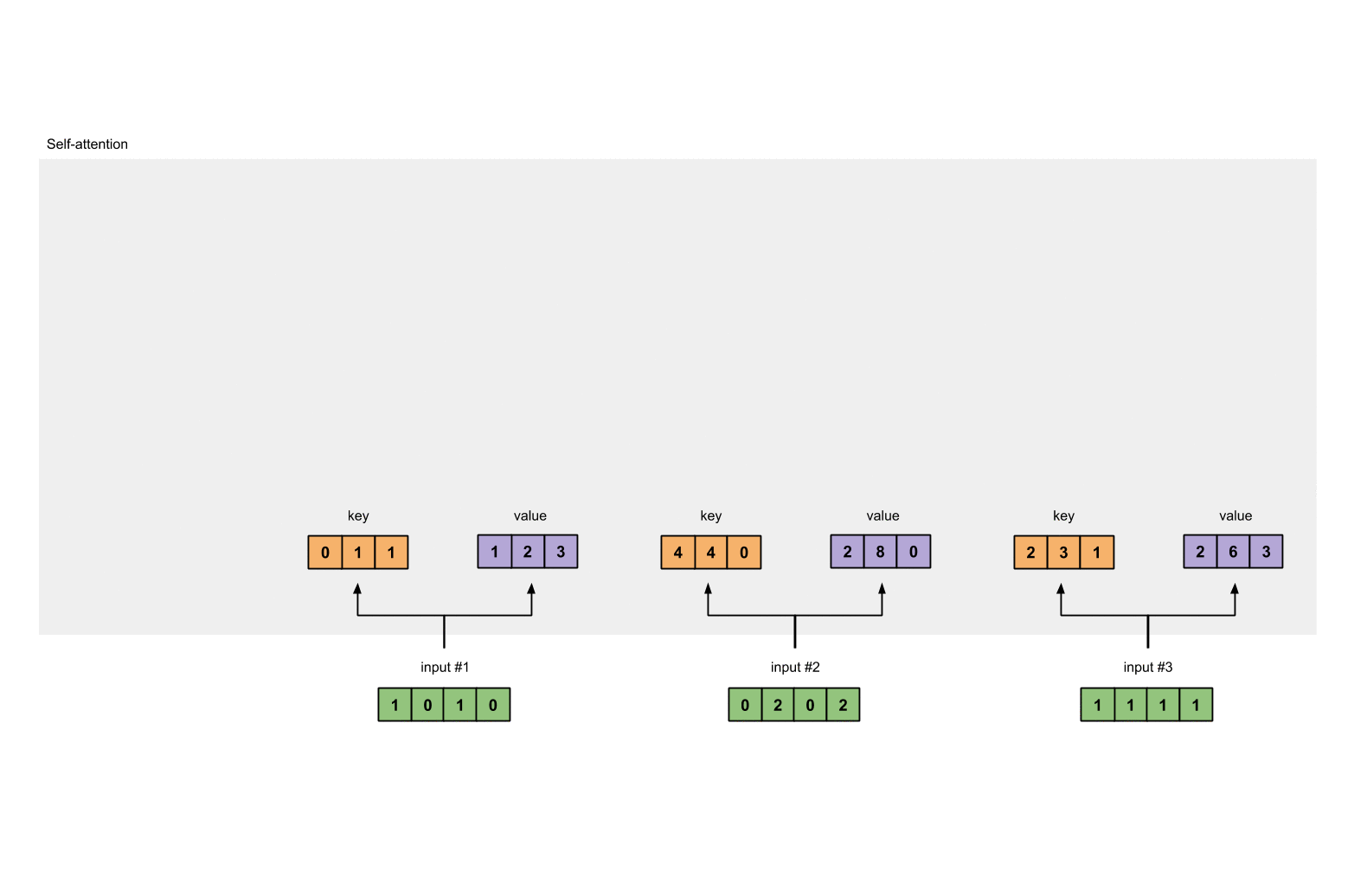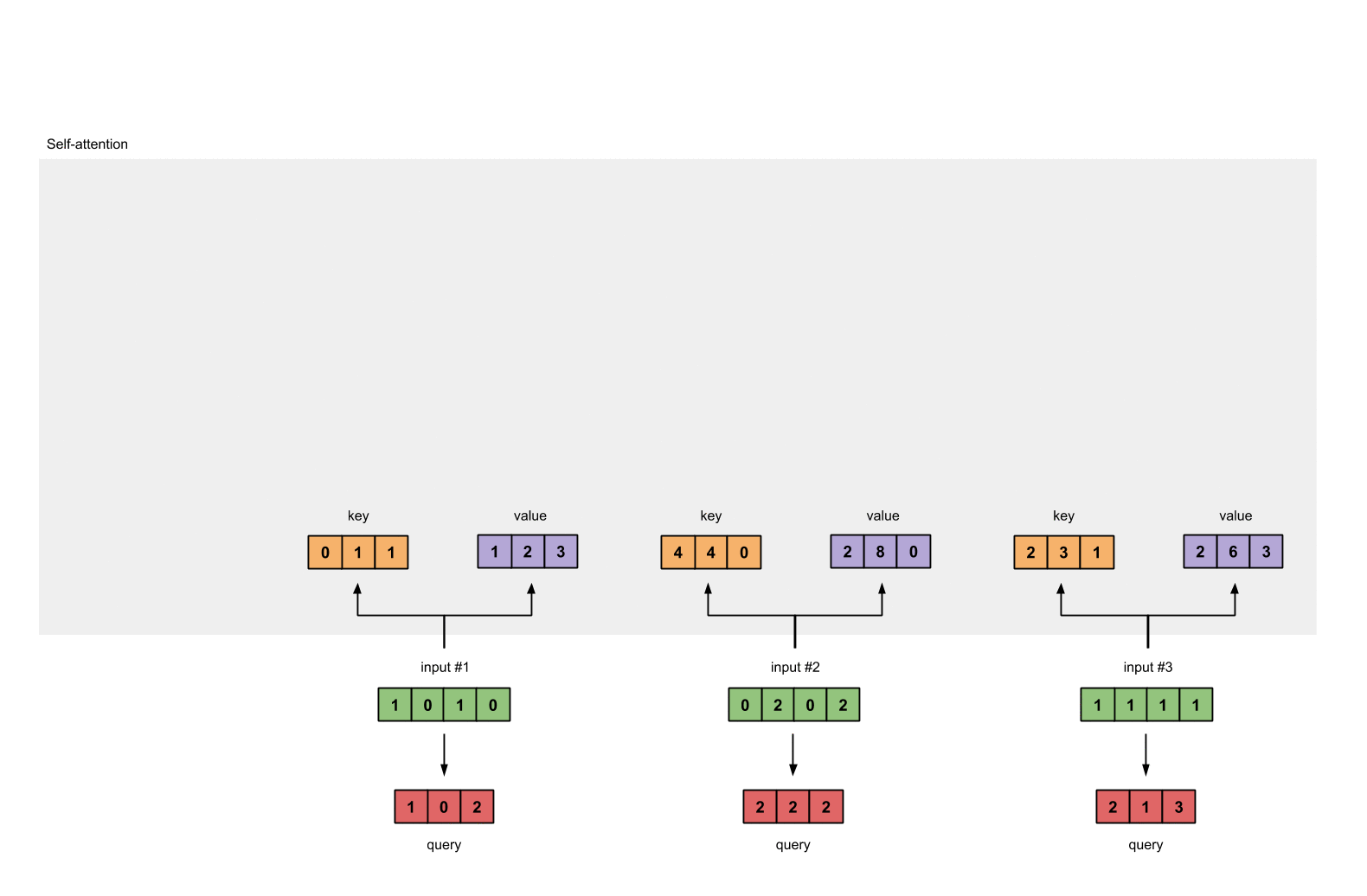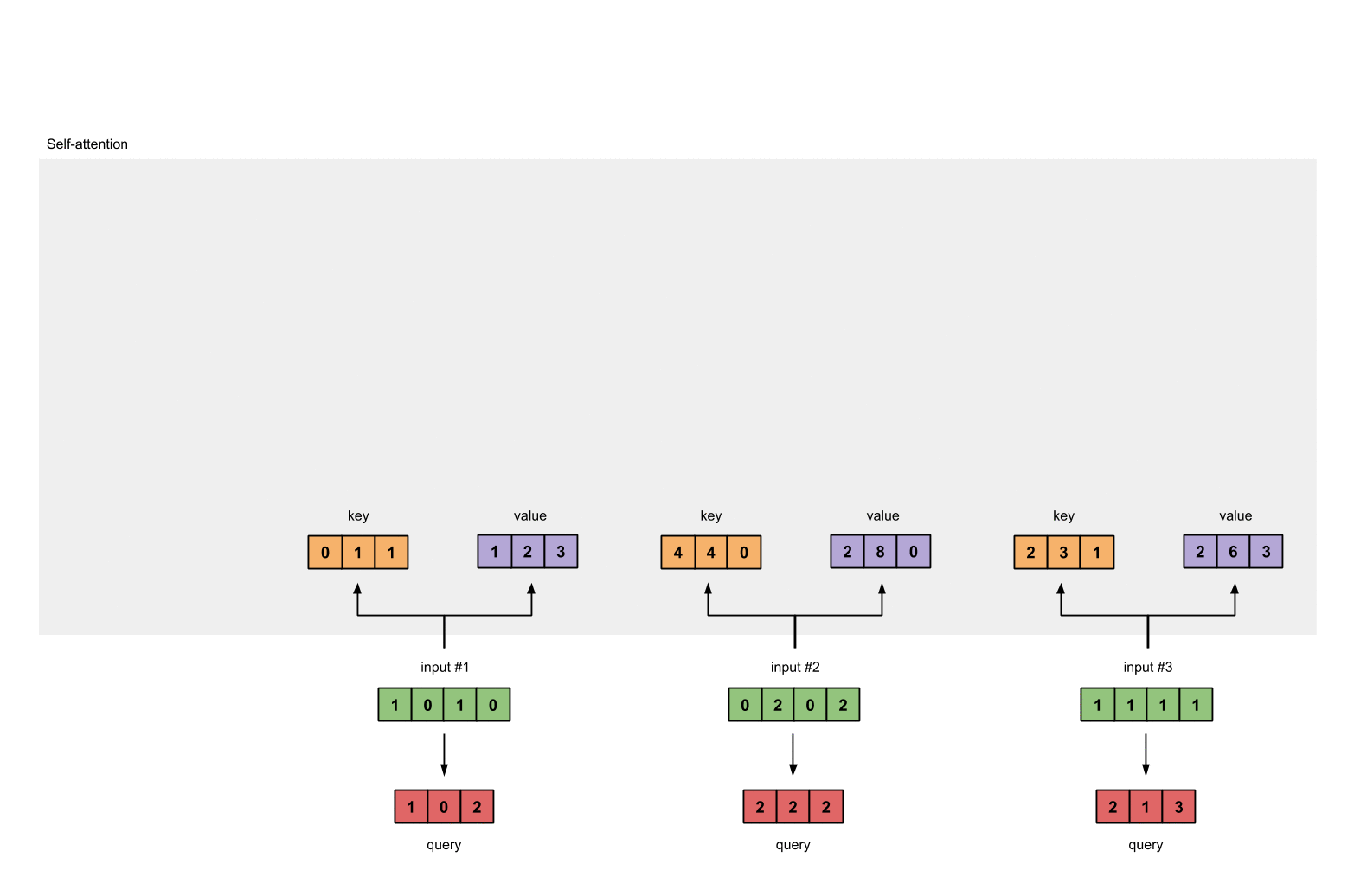
2.3 计算 key, query 和 value
现在我们计算 key, query 和 value 矩阵的值,计算的过程也很简单,运用矩阵乘法即可:
- key = input * w_key;
- query = input * w_query;
- value = input * w_value;
1 | keys = x @ w_key |
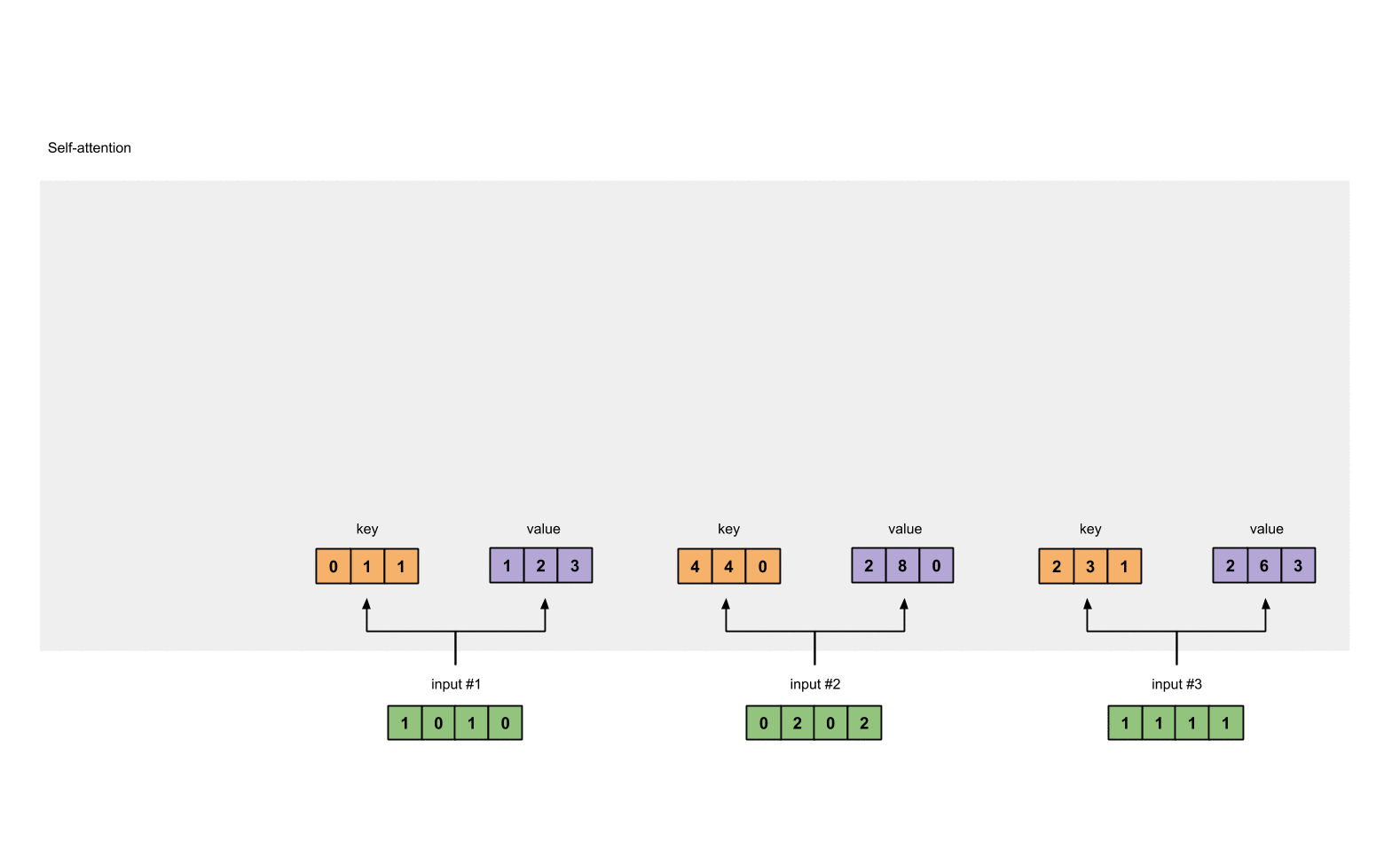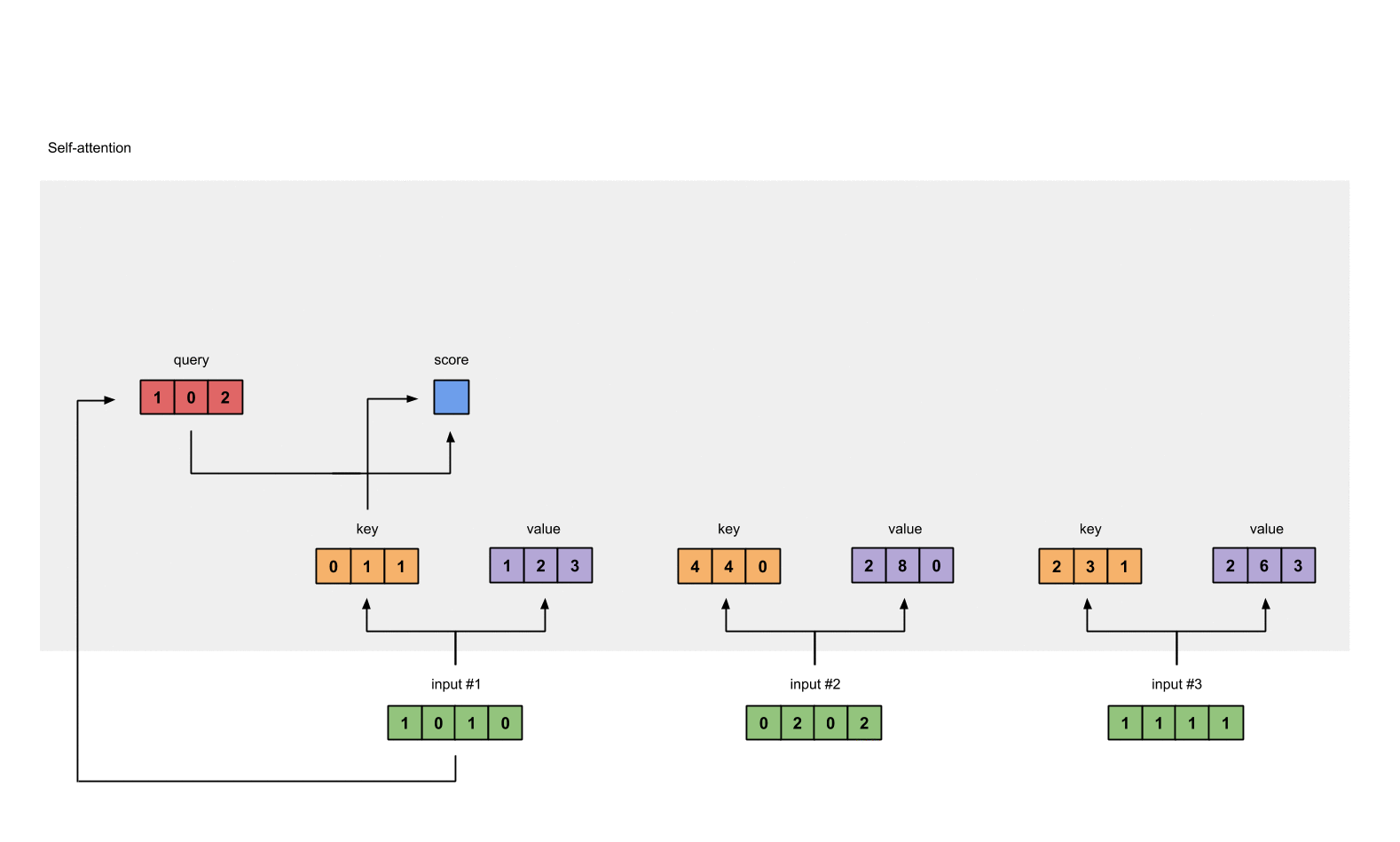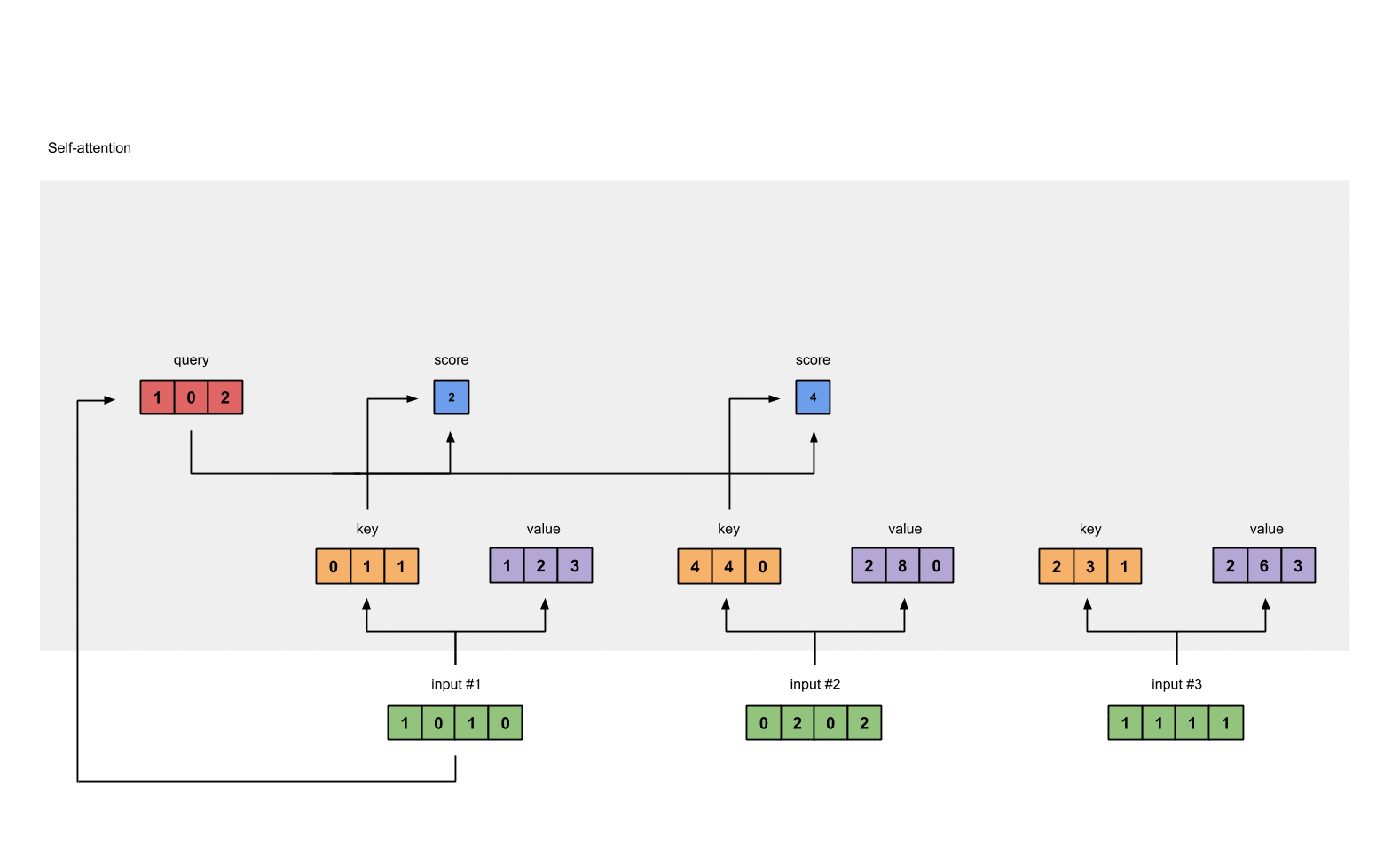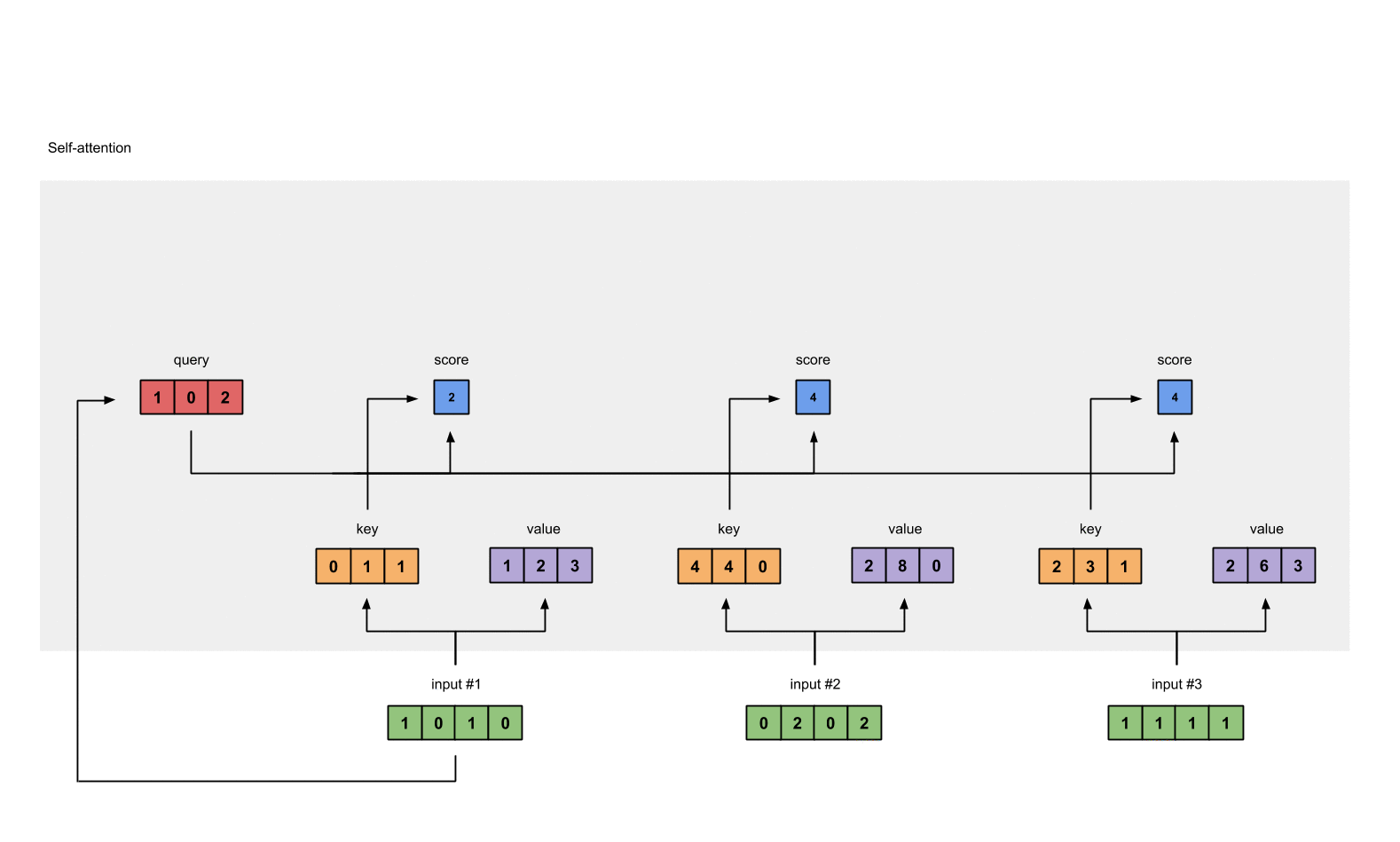
2.4 计算 attention scores
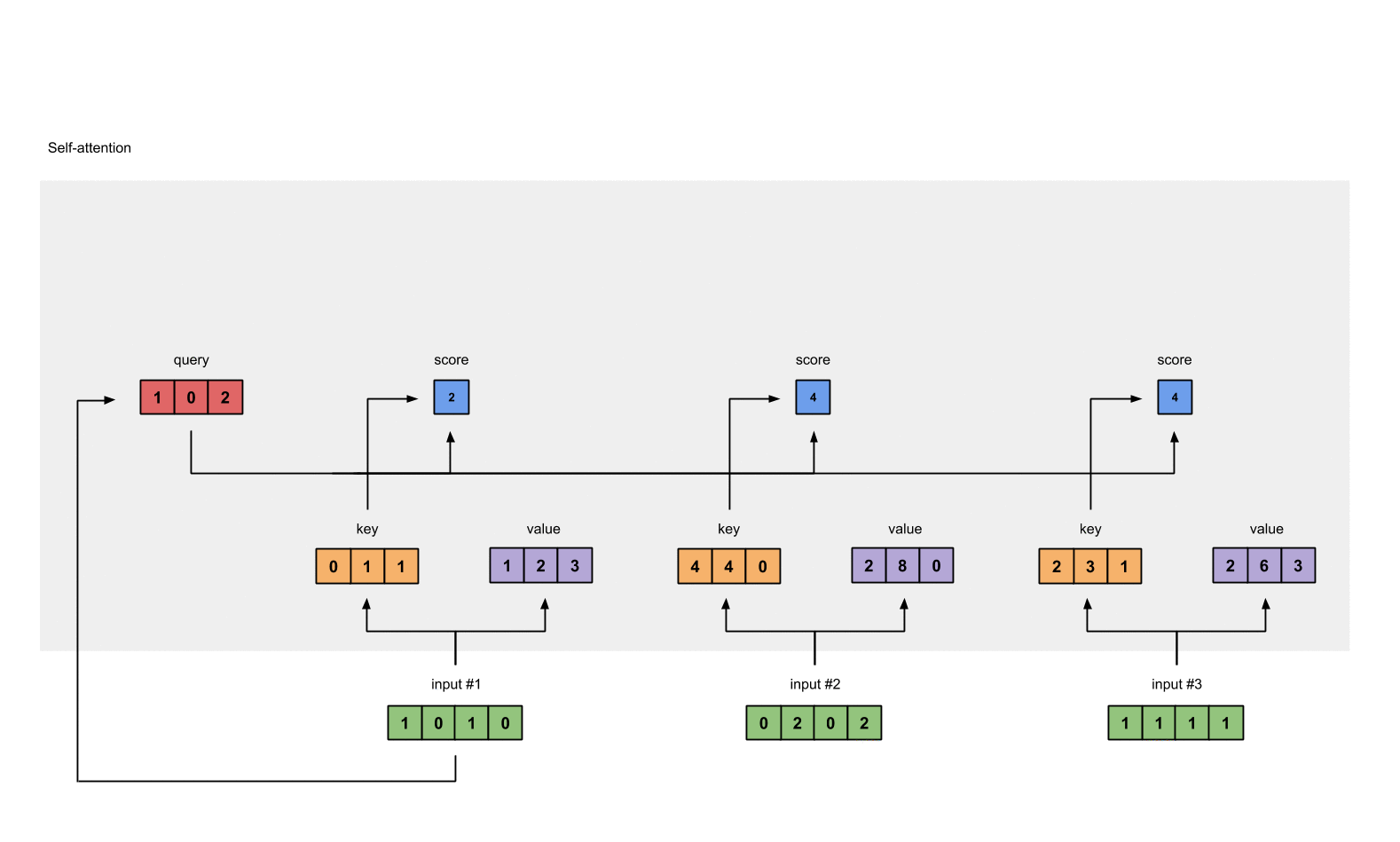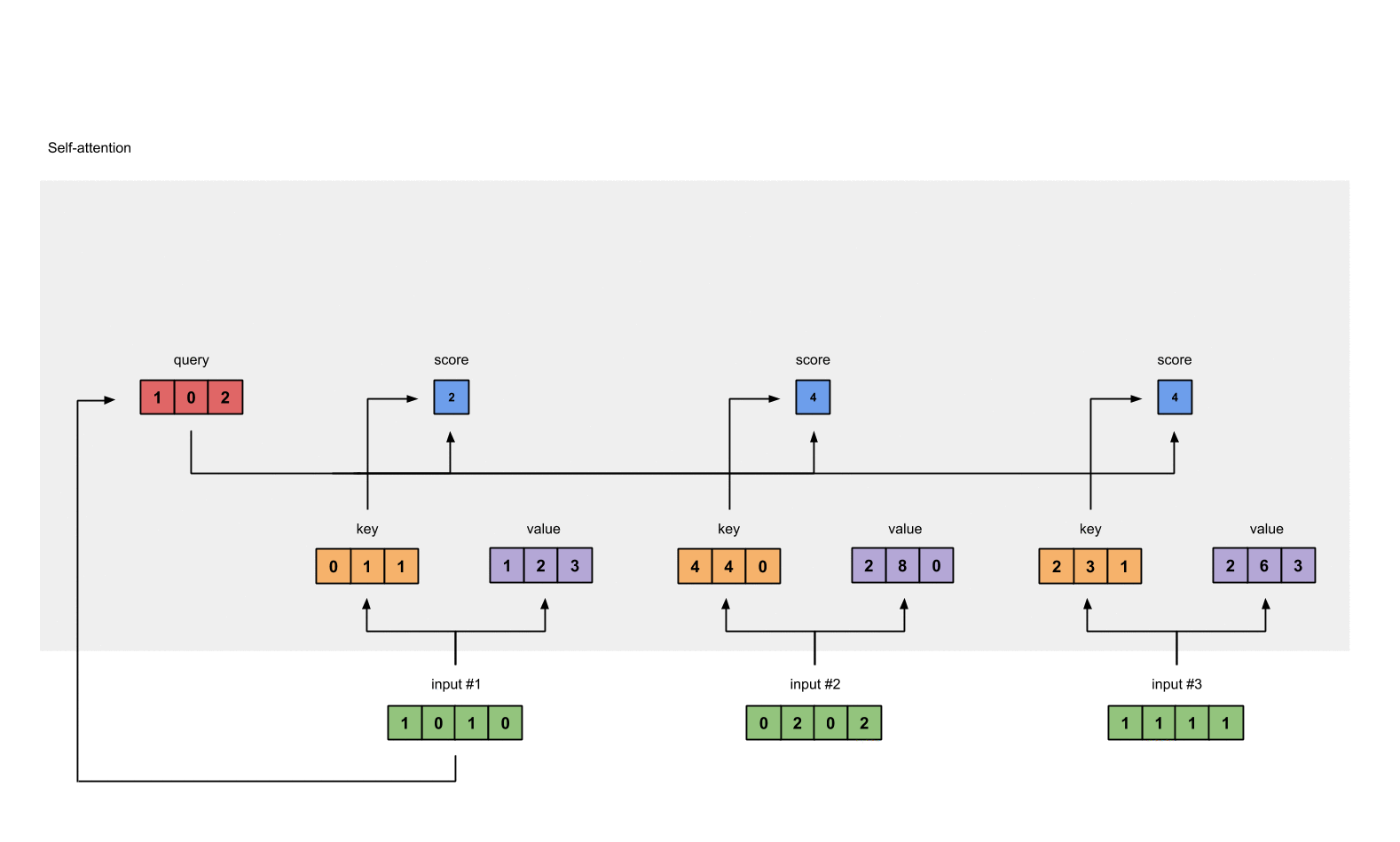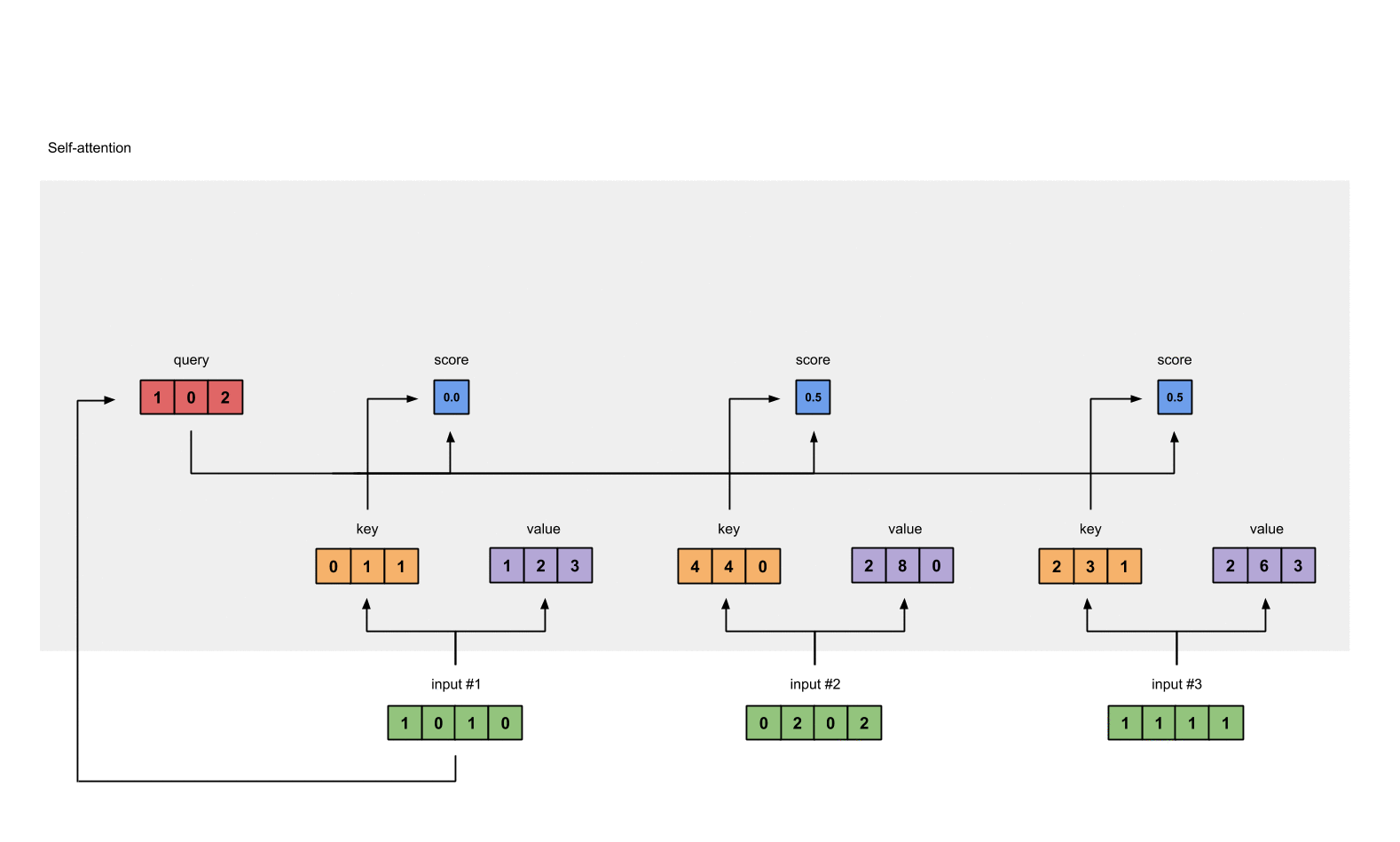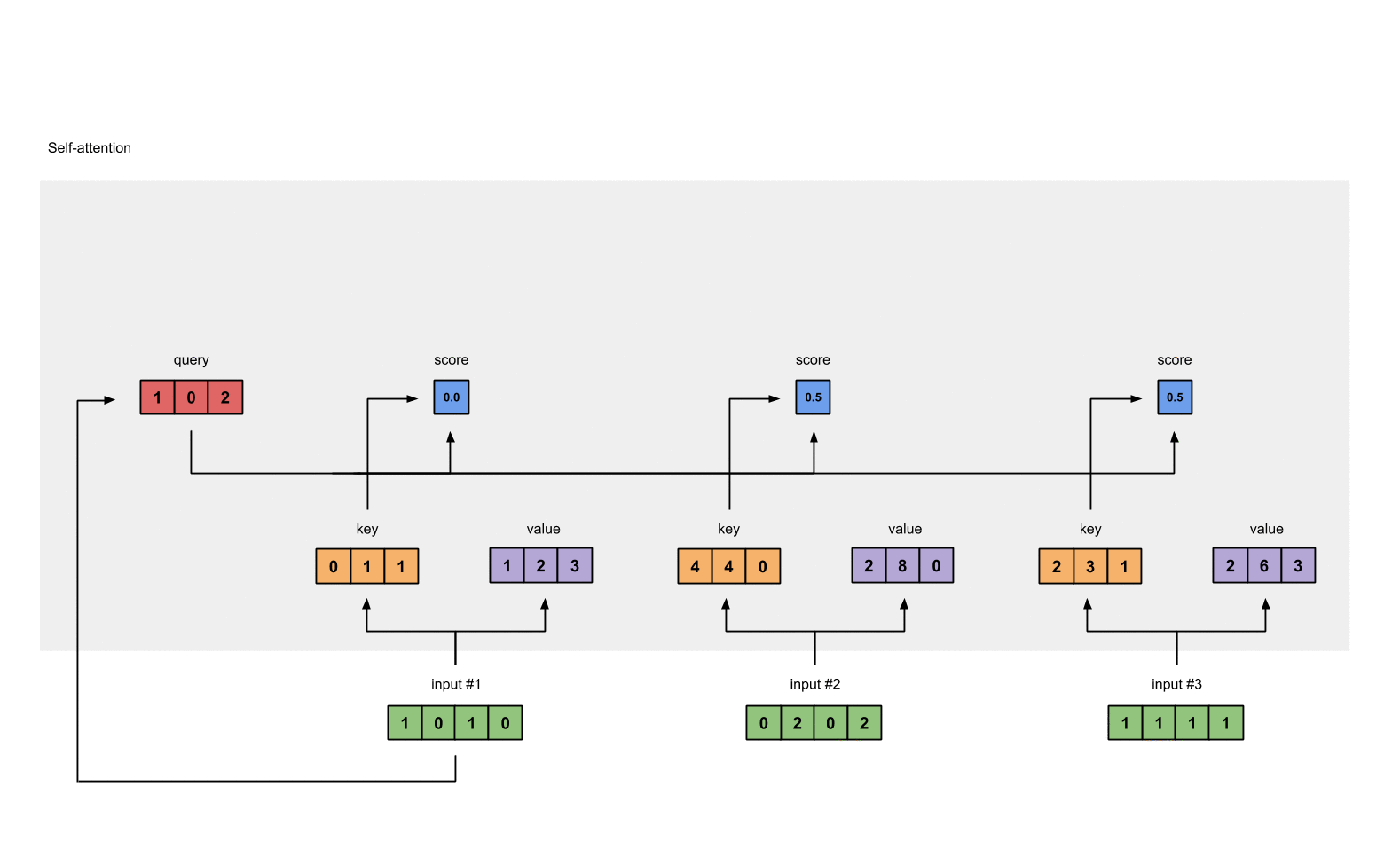
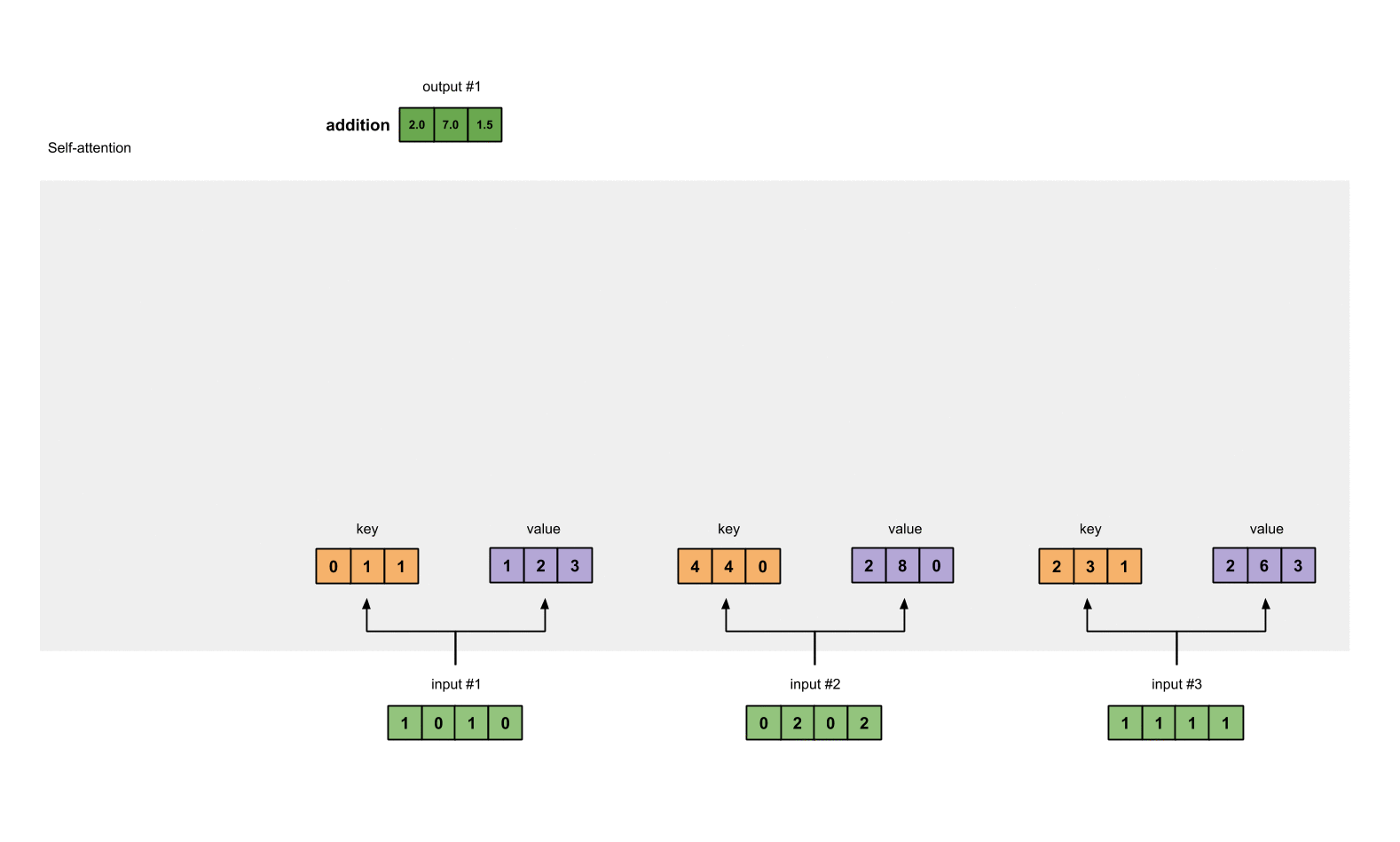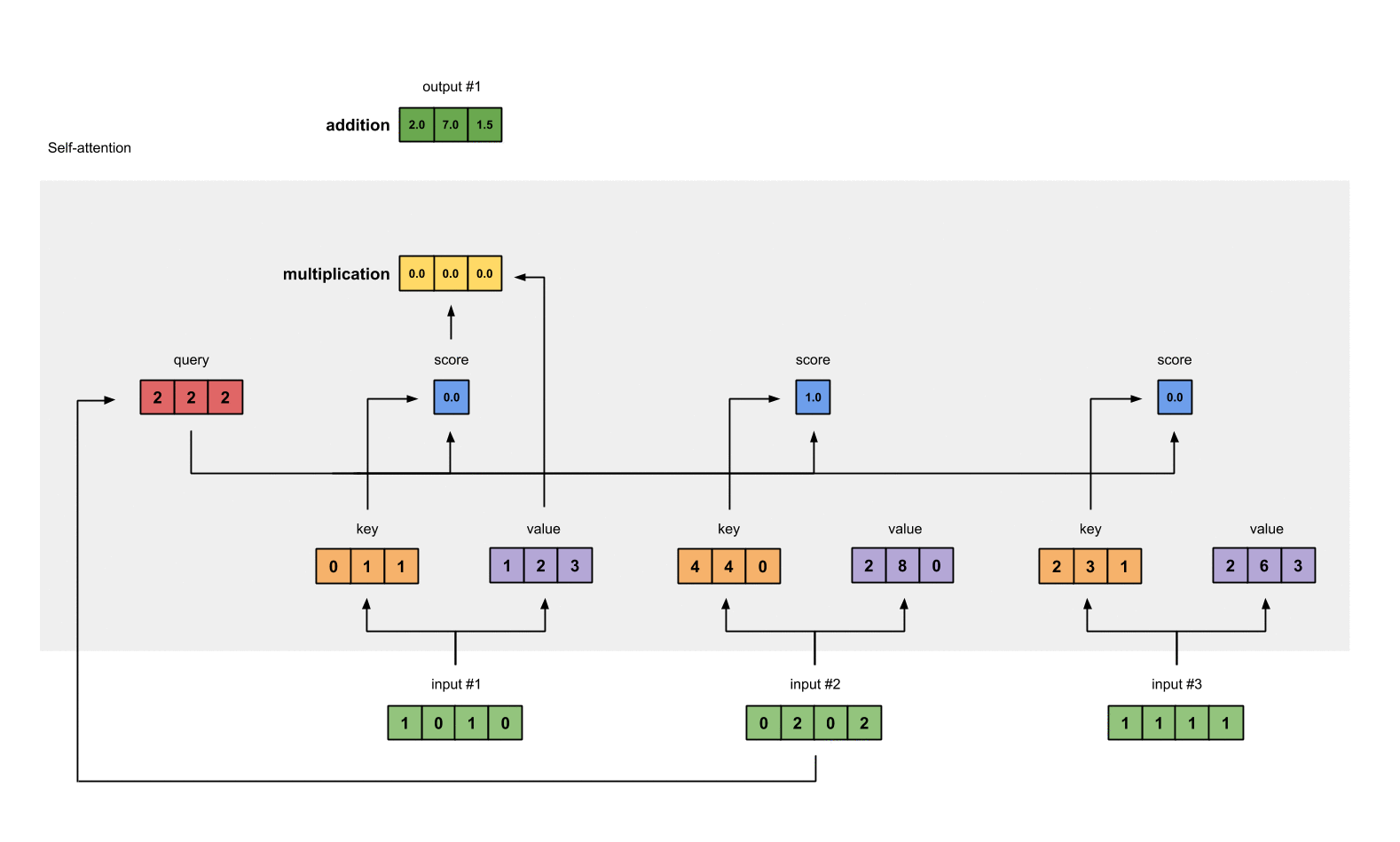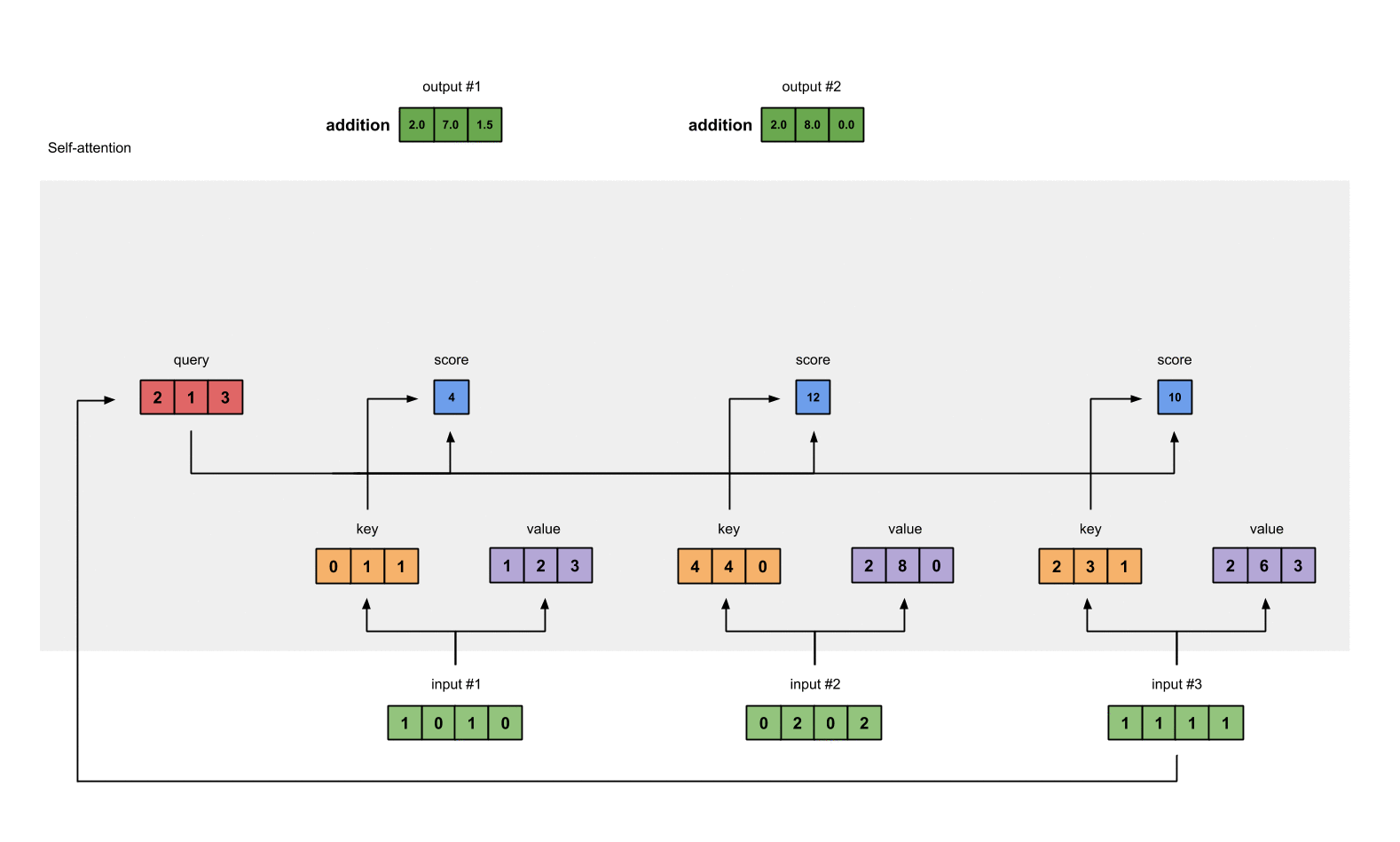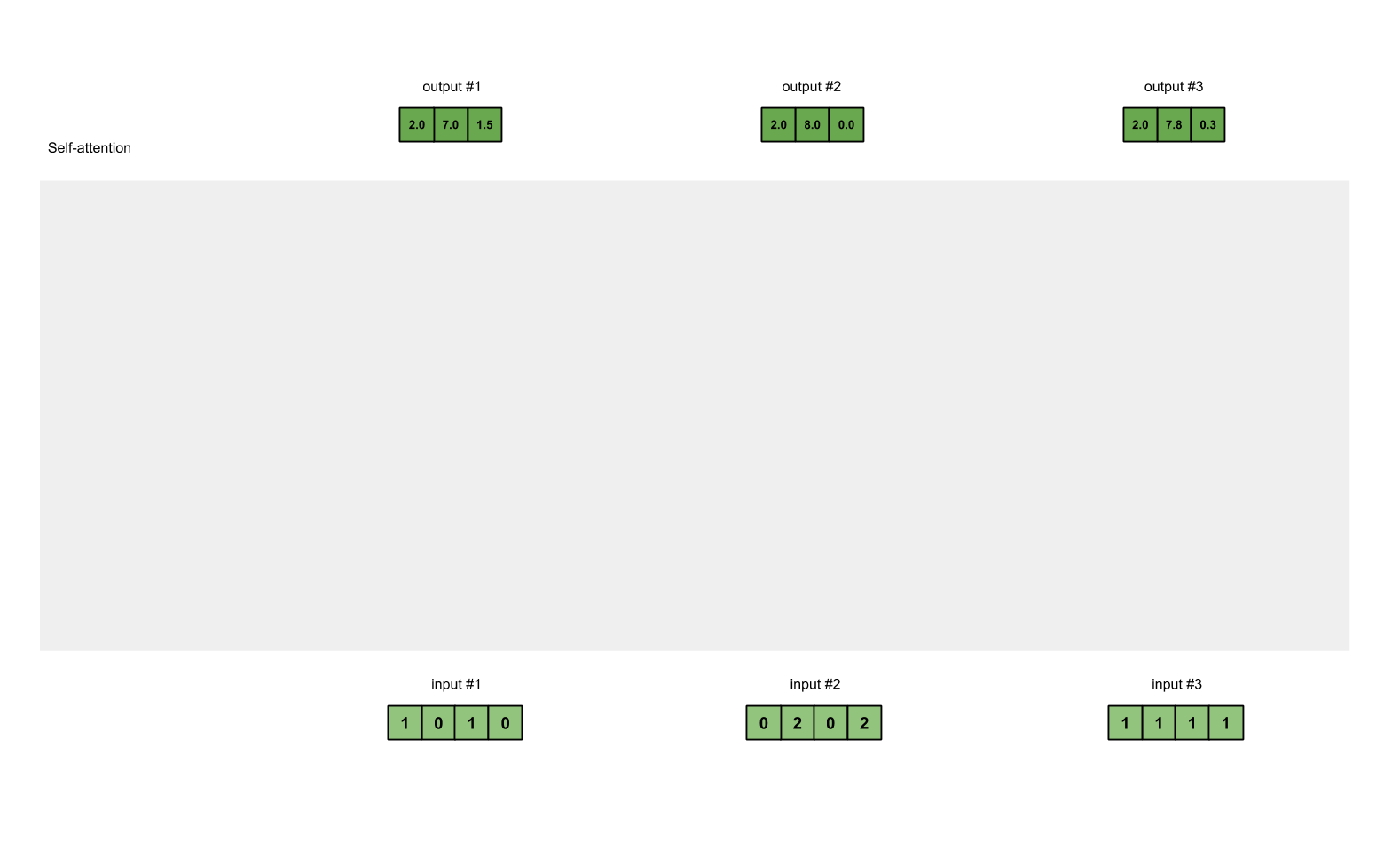
例如:为了获得 input1 的注意力分数 (attention scores),我们将 input1 的 query(红色)与 input1、2、3 的 key(橙色) 的转置分别作点积,得到 3 个 attention scores(蓝色)。 同理,我们也可以得到 input2 和 input3 的 attention scores。
1 | attn_scores = querys @ keys.T |
2.5 对 attention scores 作 softmax
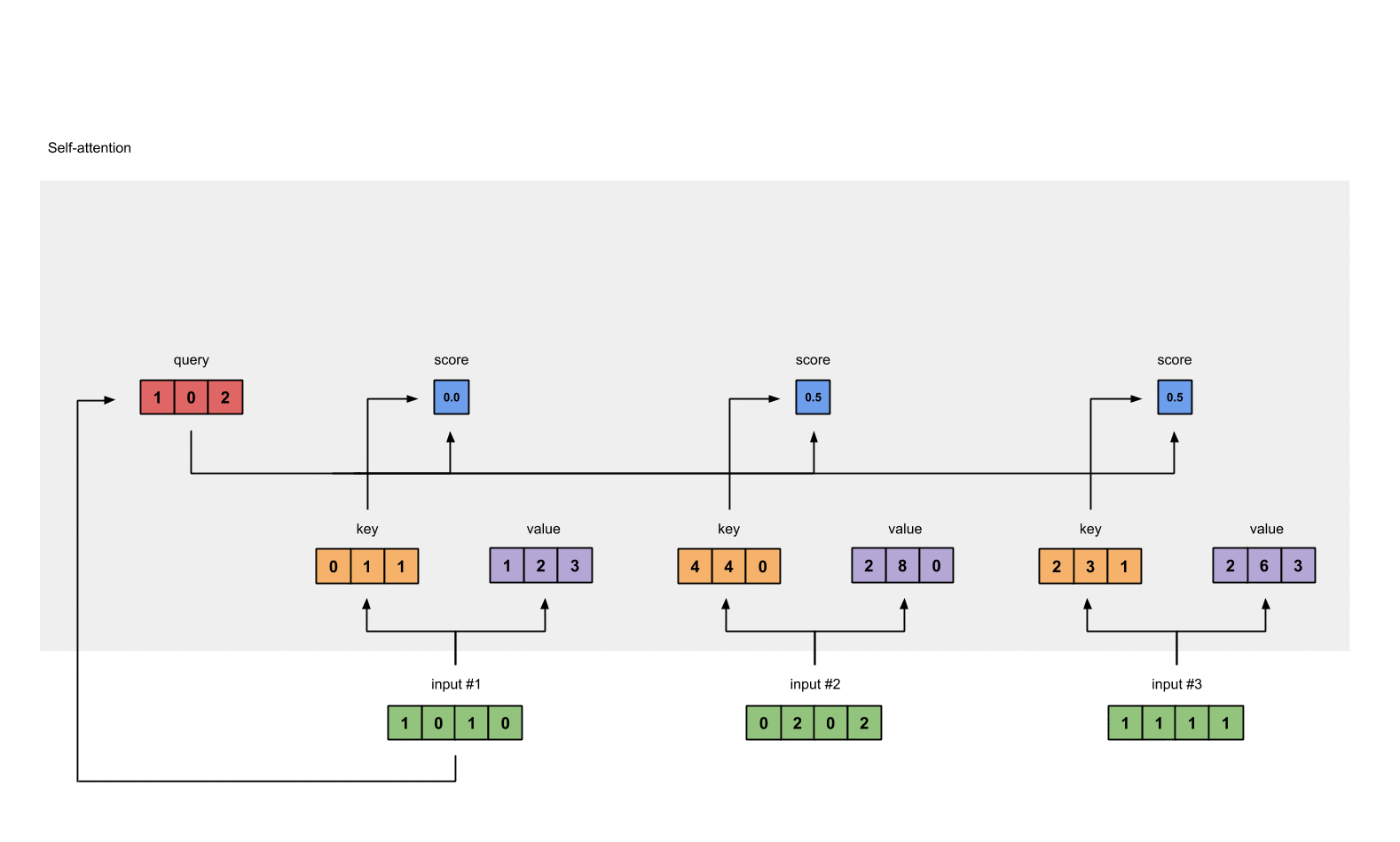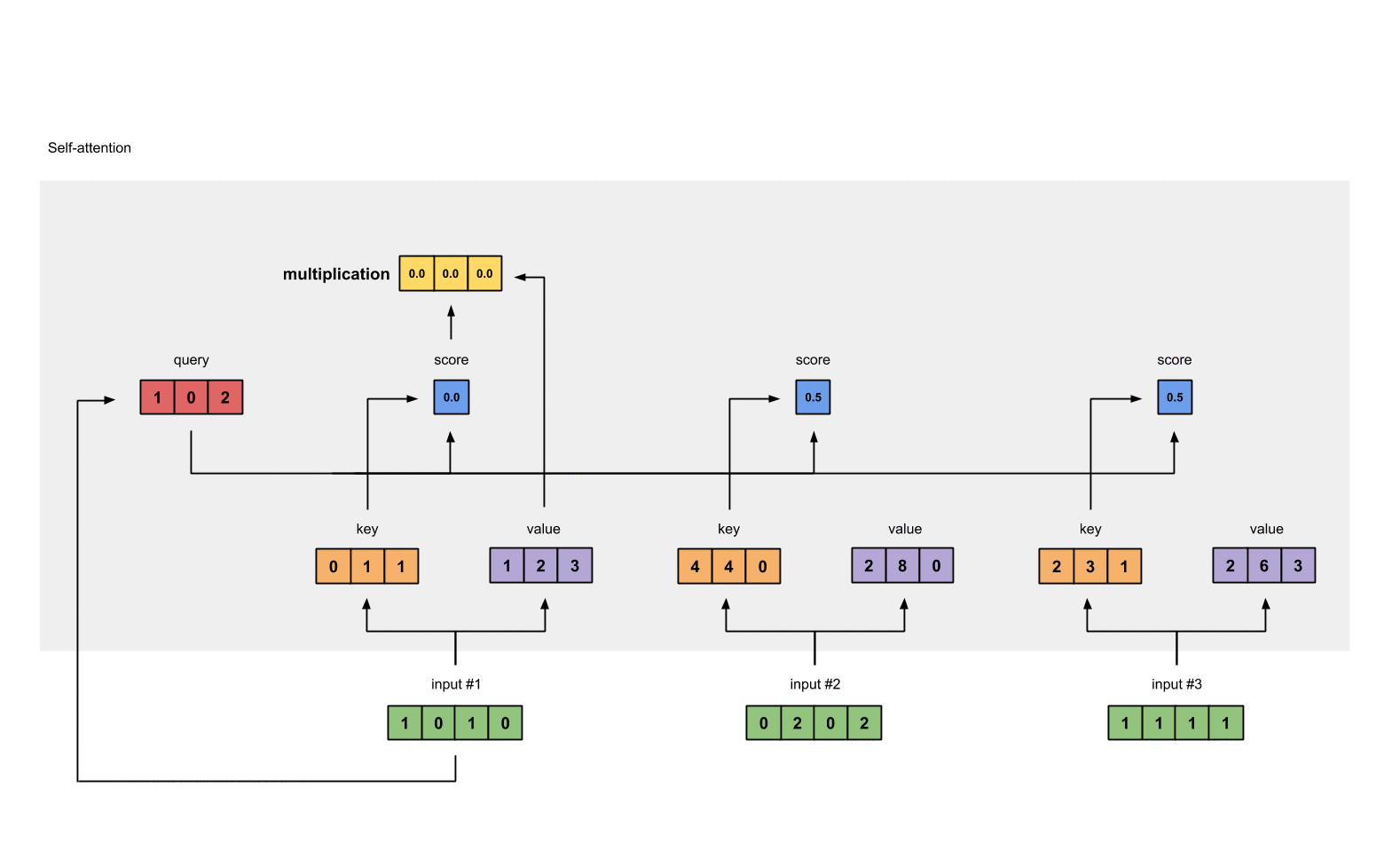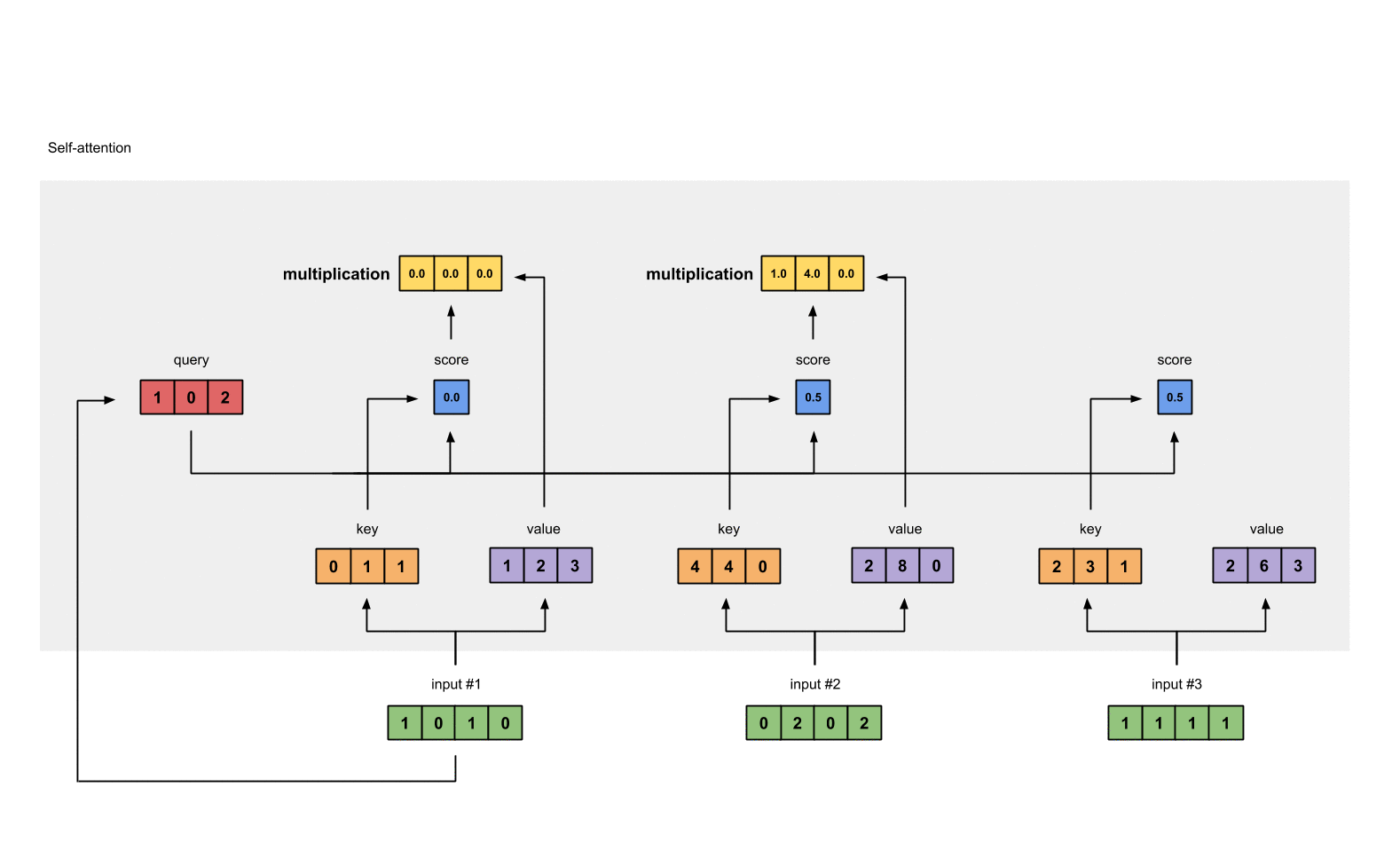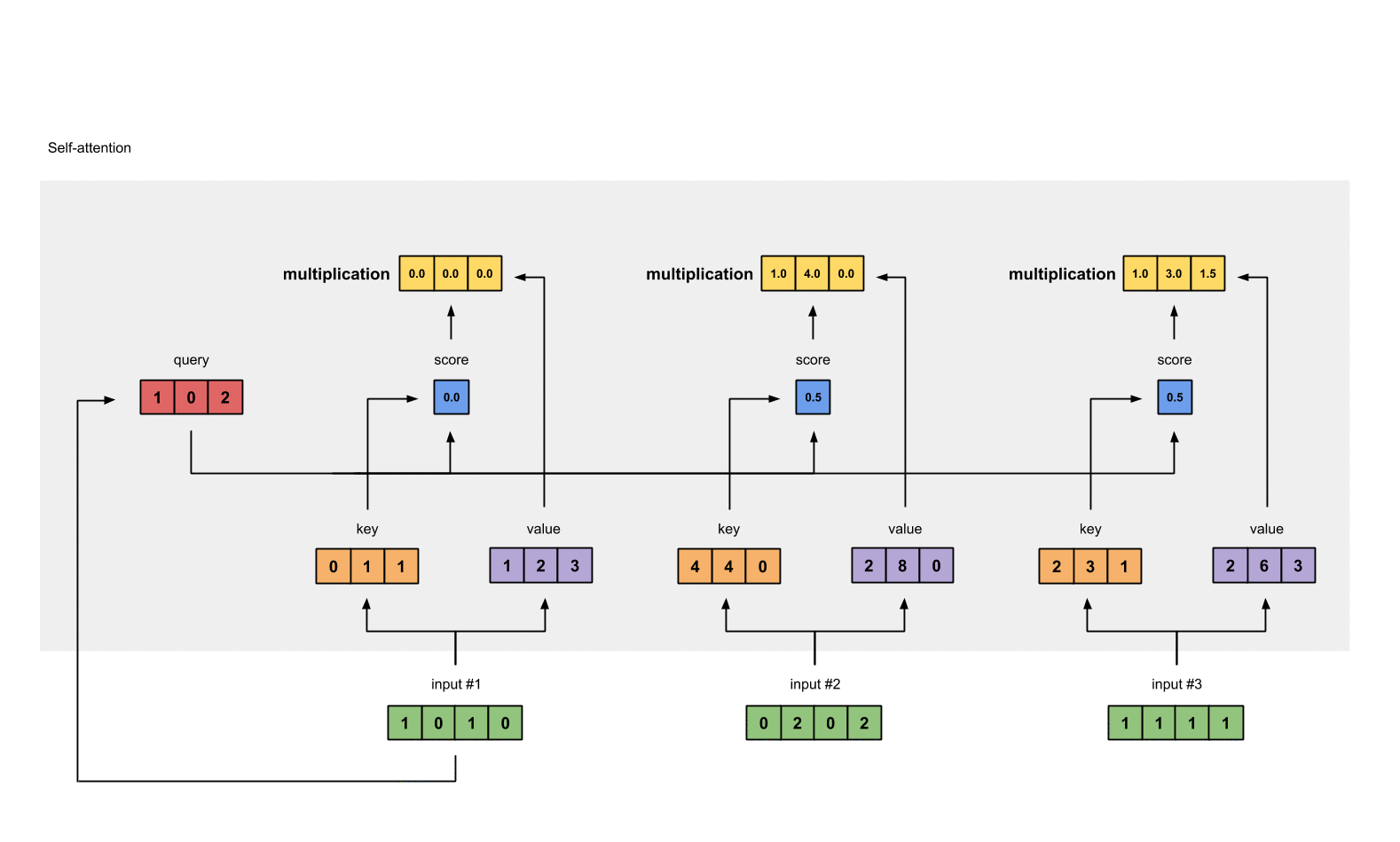
上一步得到了 attention scores 矩阵后,我们对 attention scores 矩阵作 softmax 计算。softmax 的作用为归一化,使得其中各项相加后为 1。这样做的好处是凸显矩阵中最大的值并抑制远低于最大值的其他分量。
1 | from torch.nn.functional import softmax |
2.6 将 attention scores 与 values 相乘
每个 score(蓝色)乘以其对应的 value(紫色)得到 3 个 alignment vectors(黄色)。在本教程中,我们将它们称为 weighted values(加权值)。
1 | weighted_values = values[:,None] * attn_scores_softmax.T[:,:,None] |
2.7 对 weighted values 求和得到 output
从图中可以看出,每个 input 生成 3 个 weighed values(黄色),我们将这 3 个 weighted values 相加,得到 output(深绿)。图中一共有 3 个 input,所以最终生成 3 个 output。
1 | outputs = weighted_values.sum(dim=0) |
3. 回到论文
我们在 Attention is all you need 这篇论文中,可以看到这样一个公式:
$$
Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V
$$
其实,这个公式就是描述了我们上面计算的过程。我们首先将 Query 与 Key 的转置作点积,然后将结果除以 $\sqrt{d_k}$ ,再作 softmax 计算,最后将计算的结果与 Value 作矩阵乘法得到 output。
这里有一个点,就是为什么要除以 $\sqrt{d_k}$?$d_k$ 表示的是词向量的维度。我们除以 $\sqrt{d_k}$ 是为了防止 $QK^T$ 值过大,导致 softmax 计算时上溢出 (overflow)。其次,使用 $d_k$ 可以使 $QK^T$ 的结果满足期望为 0,方差为 1 的分布。
4. 为什么这样计算?
最后的问题是,为什么要像公式那样计算呢?
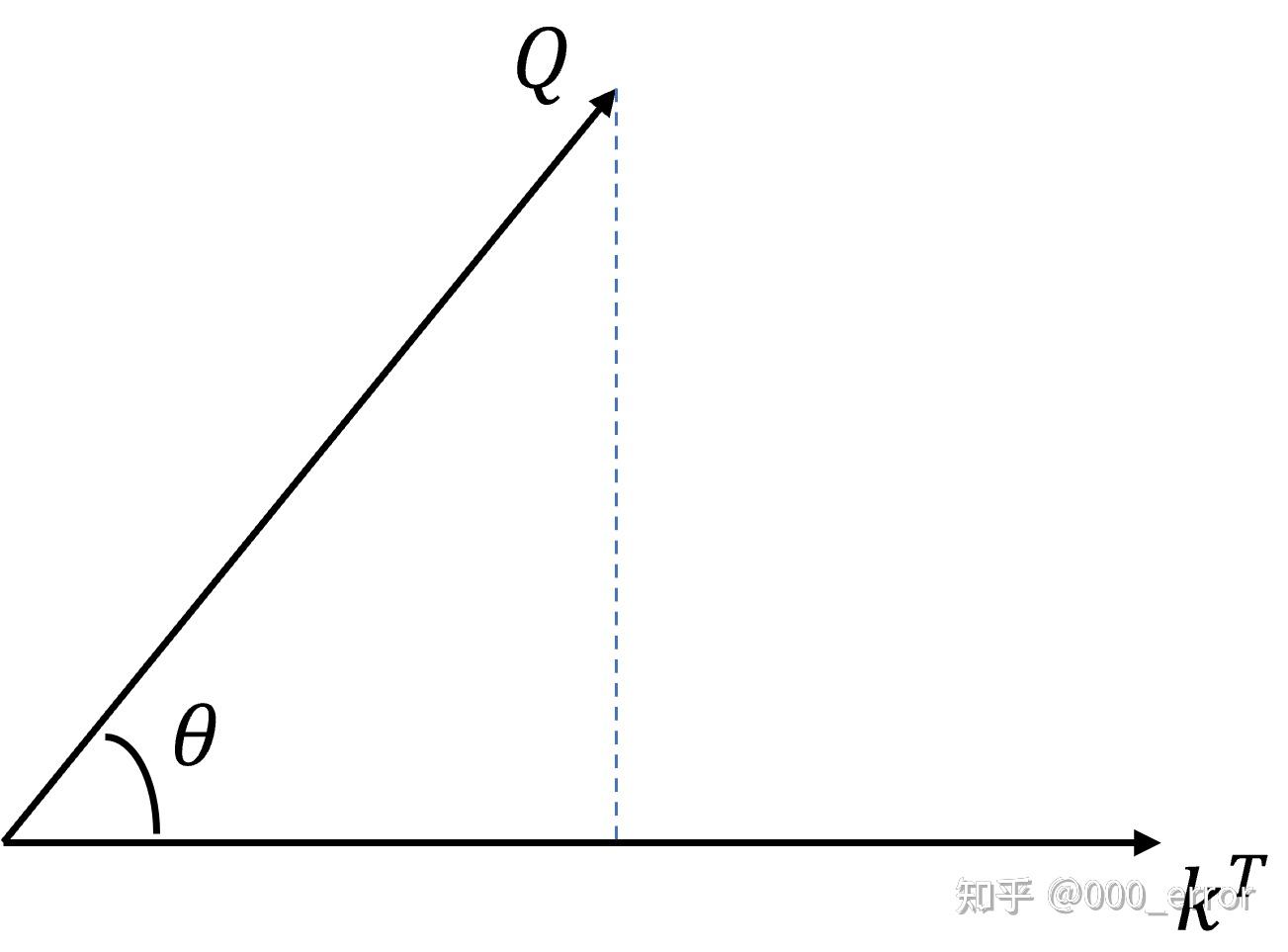
我们先从 $QK^T$ 看起,从几何角度看,点积是两个向量的长度与它们夹角余弦的积。
- 如果两向量夹角为 90°,那么结果为 0,代表两个向量线性无关。
- 如果两个向量夹角越小,两向量在方向上相关性也越强,结果也越大。
点积反映了两个向量在方向上的相似度,结果越大越相似。
对 $QK^T$ 进行相似度的计算后,再使用 softmax 归一化。最后将归一化的结果与 $V$ 作乘法,计算的结果就是输入经过注意力机制加权求和之后的表示。
5. 参考文献
- 详解 Transformer:https://zhuanlan.zhihu.com/p/48508221
- 超详细图解 Self-Attention:https://zhuanlan.zhihu.com/p/410776234
- Attention 机制与 Self-Attention 机制的区别:http://t.csdn.cn/GFTC2
- Illustrated: Self-Attention:https://towardsdatascience.com/illustrated-self-attention-2d627e33b20a
- self-attention 为什么要除以根号 d_k:http://t.csdn.cn/oaOIq