OpenAI 的 GPT 系列模型，包括其它科技公司研发的各种最先进的 NLP 模型，甚至图像处理模型，广泛采用了 Attention 注意力机制进行建模，它可谓是当前 NLP 神经网络的灵魂机制。

Original Paper：Attention is All You Need !

Recommended Post：Self-Attention Principle

OpenAI 的 GPT 系列模型，包括其它科技公司研发的各种最先进的 NLP 模型，甚至图像处理模型，广泛采用了 Attention 注意力机制进行建模，它可谓是当前 NLP 神经网络的灵魂机制。

注意力机制的思想

相信大家在学生时期，都被家长或老师提点过：“听课的时候注意力集中点！不要东张西望！” 这里就用到了注意力机制。这句话的含义是，学生应当把注意力集中在接收课堂知识上，而不是放在无关的信息上。

注意力机制的思想实际上广泛应用在各个方面，它可以抽象为如下形式：

一个智能体（人或 AI 模型）从接收到的大量信息（文本、图像、音频）中，剔除不重要、不相关的信息，重点关注与自身密切相关的信息。其核心在于收缩关注的信息范围，实现信息的压缩。

根据第 3 节的介绍，在 NLP 中，ChatGPT 语言模型建模实际上是寻找输入文本的上下文关联关系。例如：

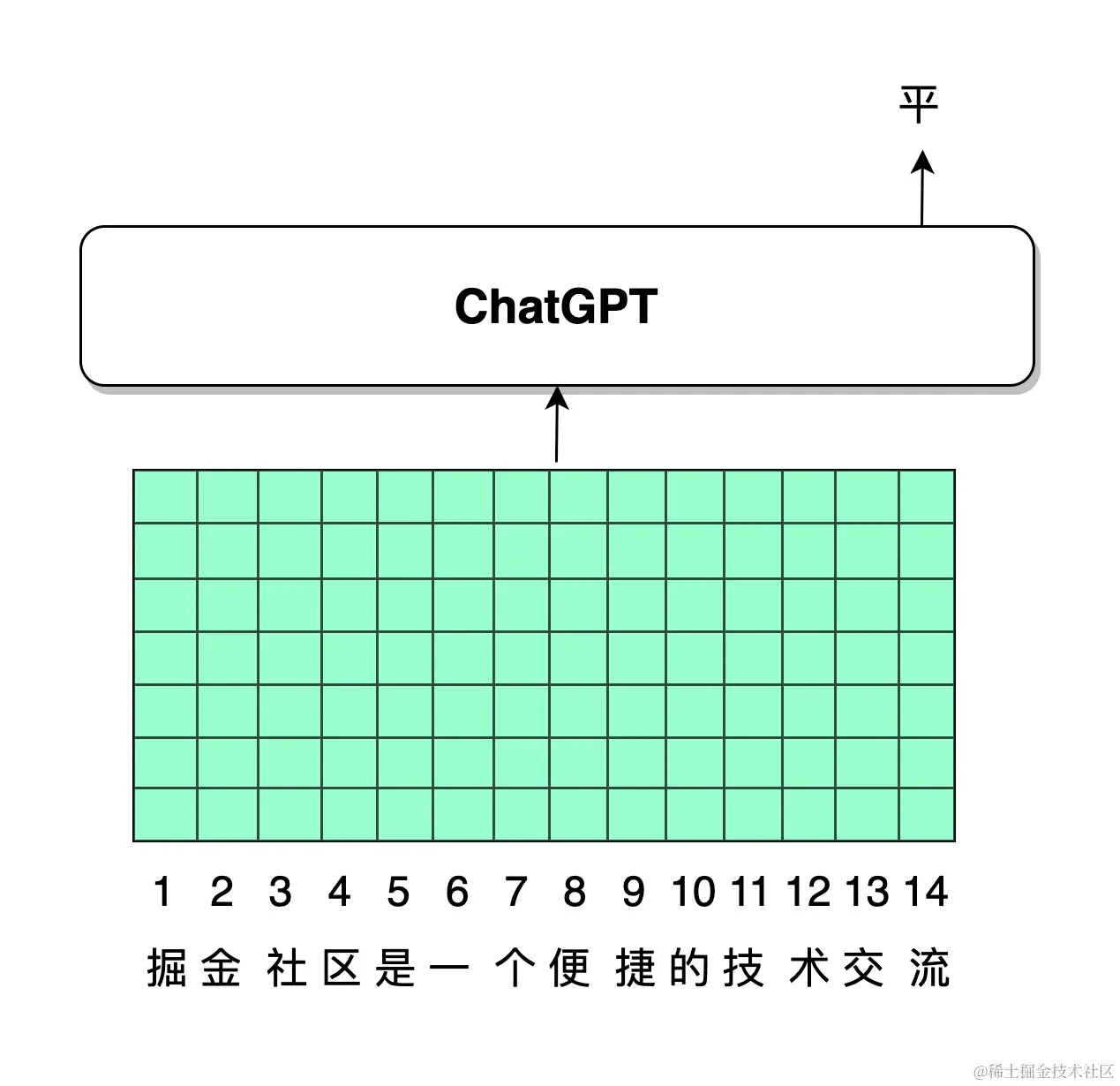
例2：请补全这条语句：掘金社区是一个便捷的技术交流______

在这条文本中，想要补全最终的语句，应当参考前文的信息，而前文总共 14 个字，对空格处影响最大的是掘金两个字，而像形容词便捷的，系词是一个都不是最关键的影响因素。换句话说，我们应当设计一种注意力机制，让模型能够在输出空格字符的时候，最大限度地注意到掘金两个字。

注意力机制的建模

建立权重模式

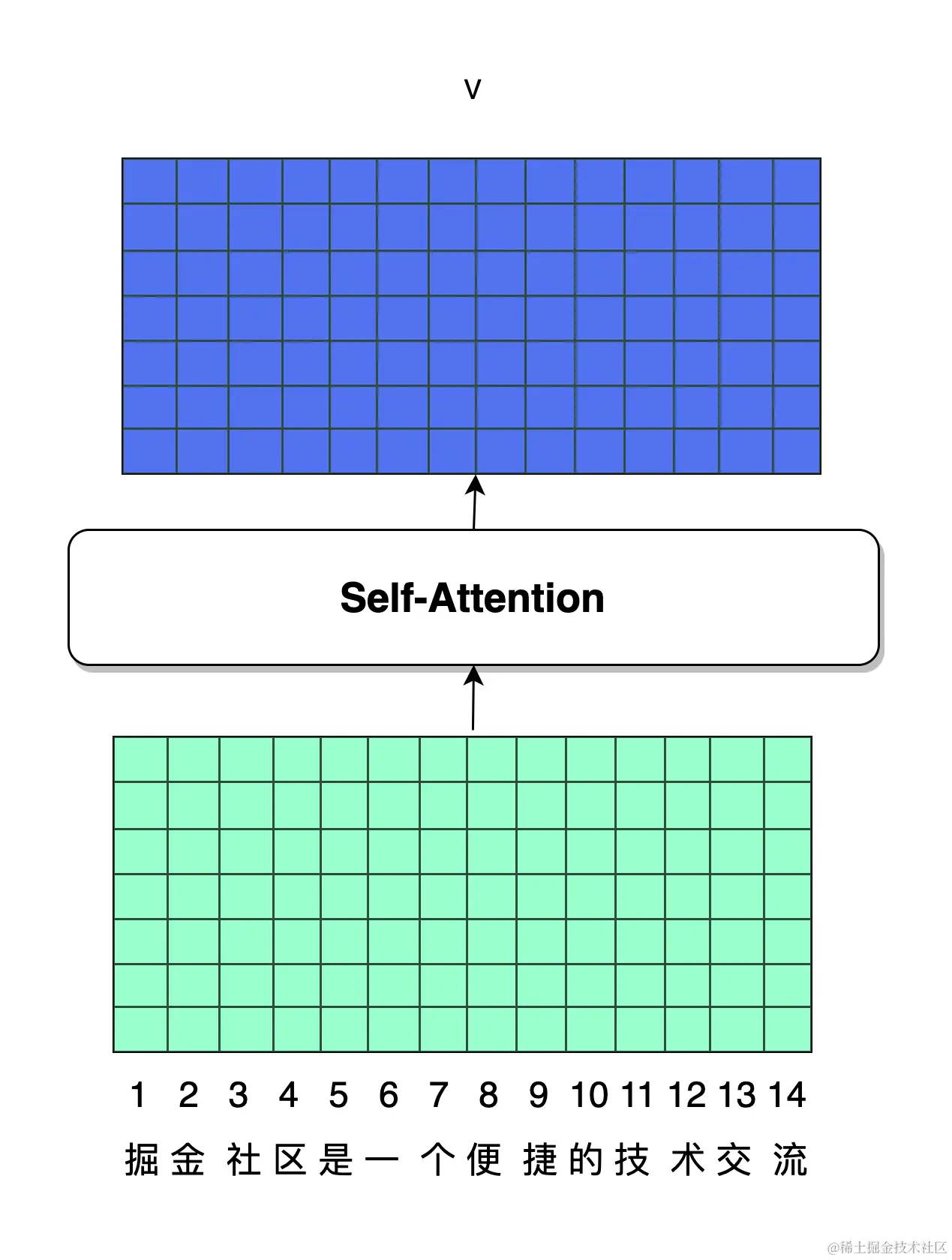
根据第 4 节的介绍，在 NLP 模型中，自然语言是以 token 形式排列输入模型中的。如下图所示，绿色的每一列都是对应的一个 token 的 embedding 向量表示，假设每一个 token 的 embedding 具有 7 维，总共 14 个 token 共同组成一个 embedding 矩阵。我们的模型设计思路，是模型应当能够在输出平台的平 字时，更加关注到掘金二字。

5-1.png

让模型更加关注到掘金两个字，实际上可以认为，给掘金两个字对应的 token embedding 赋予更大的权重。

在神经网络模型中，所有的操作均为矩阵操作，所有的特征均为向量形式。设 $e_i$ 表示第 $i$ 个 token 的 embedding 表示，在例子中，它是一个 7 维的向量，$w_i$ 是第 $i$ 个 token 对应的权重值，它是一个标量值。那么，可以对所有的 token embedding 做一个加权：
$$
h=\sum_ie_iw_i
$$
这里，$h$ 是一个加权后的结果，它也是一个 7 维的向量。它的本质含义，是从各个 token 不同的 embedding 中，按重要程度（权重值 $w_i$）做加和，权重值高的 $e_i$ ，对后续操作影响大，权重值低的 $e_i$ ，对后续操作影响小。这就产生了一种更加注意权重高的 $e_i$ 的效果。

softmax 函数

定义：softmax 函数是在机器学习和深度学习中广泛使用的一个非常重要的函数，尤其是在处理分类问题时。它可以将一个含任意实数的K维向量压缩（映射）成另一个 K 维实向量，其中每个元素的范围都在 $(0, 1)$ 之间，并且所有元素的和为 1。因此，softmax 函数的输出可以被视为一个概率分布。

公式：$Softmax(z_i)=\frac{e^{z_i}}{\sum^K_{j=1}e^z j}$

作用和特点：softmax 函数的输出可以解释为一个概率分布，每个元素的值代表了对应类别的概率。使用指数函数确保所有的输出都是正的，并且可以放大输入向量中的差异。softmax 函数配合交叉熵损失函数，常用于训练阶段的梯度下降优化。这种组合可以给出明确的梯度信息，有利于模型通过学习数据来调整参数，以提高分类的准确性。

应用场景：

  • 多类分类问题：在神经网络的最后一层，用于将神经元的输出转换为预测每个类别的概率。
  • 语言模型：在处理自然语言处理任务，如文本分类或机器翻译时，softmax 被用来预测下一个词的概率分布。
  • 增强学习：在某些策略梯度方法中，softmax 用于从一组可能的动作中选择动作。

上面的加权计算中，$w_i$ 是一个标量值，假设模型经过训练后，针对上述例子的 token 计算得到：$w=(w_1,w_2,\ldots,w_i,w_{14})=(2.1,1.3,\ldots,-1.2,-0.4)$

其中的数值有正有负，前两个 token 对应的权重标量值较大，说明对后续操作的影响大。若直接进行加权，这不符合人们的一般认知。一般来说，权重占比以概率形式表示，概率值应当大于 0，小于 1，且所有分量的加和等于 1。

例如：今年国内的 GDP 占比中，第一产业占比 14.6%，第二产业占比 35.2%，第三产业占比 50.2%。

这是一个典型的概率分布示例，其总和为1，三产占比最高，权重最大，影响经济的程度最大。

因此，我们应当将 $w$ 转换为概率占比形式，主要采用 softmax 方法：
$$
α_i=\frac{exp(w_i)}{\sum_i exp(w_i)}
$$
其中，$exp$ 是指数计算，$α_i$ 表示第 $i$ 个 token 的 embedding 对应的权重，其值介于 0~1 之间。计算上例，假设：
$$
w=(2.1,1.3,0.1,0,−0.2,−1.3,0.5,0.2,−0.8,0,0.1,−0.7,−1.2,−0.4)
$$
那么，第 1 个 token 的权重：
$$
α_1=\frac{exp(2.1)}{\sum exp(w_i)} = \frac{8.166}{8.166+3.669+1.105+1+\cdots+0.301+0.67}=\frac{8.166}{21.858}=0.374
$$

此外，其它若干 token 的权重为：
$$
α_2=\frac{exp(1.3)}{\sum exp(w_i)} = \frac{3.669}{8.166+3.669+1.105+1+\cdots+0.301+0.67}=\frac{3.669}{21.858}=0.167
$$

$$
α_6=\frac{exp(-1.3)}{\sum exp(w_i)} = \frac{0.272}{8.166+3.669+1.105+1+\cdots+0.301+0.67}=\frac{0.272}{21.858}=0.012
$$

第 1、2 个 token 对应掘金 两个字，分别占权重 37.4% 和 16.7%，占比较高，第 6 个字是一，它的 token 对应的权重仅 1.2%，占比较低。这说明，在这个模型中更加注重了掘金 的权重，方便后续模型输出正确的字符 token。

这个例子说明了 softmax 算法的一些特性：

1、softmax 可以将一维向量，输出形成概率分布的形式；

2、softmax 利用指数函数，会更加着重值更高的元素，使要关注的元素更加突出；

3、相应地，由于指数函数特性，它也可以尽力压低不需关注的元素的权重。

以公式形式表示，计算模型的所有 embedding 加权后的权重：
$$
h=\sum_i e_i α_i
$$
Softmax 函数在神经网络模型中十分常用，除了应用在注意力机制计算外，softmax 还可以完美契合交叉熵损失函数（将在第 8 节中介绍）。

自注意力机制 Self-Attention

前文讲述了，利用权重向量 $w$ 就可以找到模型要关注的重点内容。那么，$w$ 从哪来呢？值如何计算出来？

计算权重，不同的模型、不同的 NLP 任务都有不同的形式。这项技术经过多年的发展，最终趋向于自注意力机制（Self-Attention） ，这也是 ChatGPT 所采用的形式。

$w$ 是一个权重向量，其长度（维度）与 token 的个数相同，其中的每一项是标量值。我们知道，神经网络模型中都是以向量、矩阵等构成的张量作为计算基础的。因此，想要计算得到一个标量值，最简单的形式就是向量点积，我们需要想办法找到两个向量。

假设针对第 $i$ 个 token，有两个向量 $q_i$ 和 $k_i$，两者具有相同的维度，其点积可以得到一个标量值：$w_i=q_i k_i$

依然以前述句子为例。在补全句子时，掘金对要空格处填写的字符，影响最大。而“掘金对要填写什么字符，影响最大”这一认知，依然是我们阅读这个句子本身得到的。换句话说，**$w_i$ 权重的信息来源，依然是原句子本身（Self）**，这就是自注意力命名的原因。

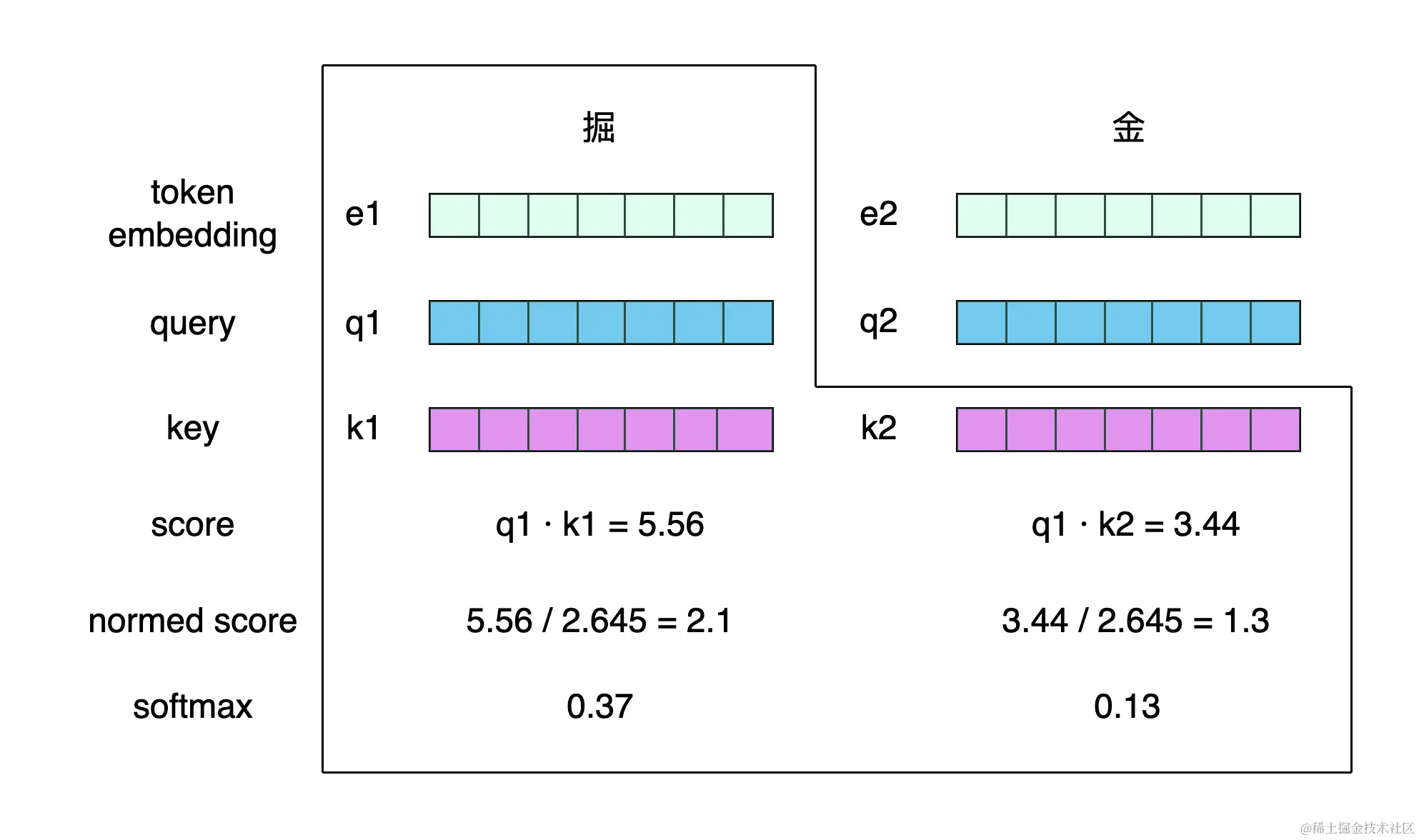
因此，我们可以直接把每个 token 的 embedding 分别当作向量 $q_i$ 和 $k_i$ 进行计算。计算过程如下图所示。

更详细的解析请见：动图轻松理解 Selft-Attention（自注意力机制）

5-2.png

当我们计算第 $i$ 个 token的 $w_i$ 值时，以第 1 个 token 掘字为例，应当先观察整条文本的 token，将所有的 token 都和 掘 token 做计算，这实际上就是在比较 掘 token 和其它 token 的关联关系。

在上图中，$q_i$ 含义为 query（中文含义为查询向量），和 $k_i$ 的含义为 key（中文含义为钥匙向量）。

为何起名 query 和 key？

query 和 key 这两个词，最初是计算机搜索引擎中提出的概念，在 AI 领域中，被引申到注意力机制上。

例如，当我们在 Google 搜索引擎中查询搜索“成都有什么好吃的？”时，搜索引擎会按匹配程度给出若干回答。

其中，用户的搜索问句，就被称为 query，而每一条匹配到的结果，都包含和 query 的关联性，也就是各自的 key。通过 query 和 每一条 key 的匹配，就可以得到问答搜索结果的匹配程度。

回到上图中，当计算 掘 token 的输出向量时，即利用其 query 向量，分别和每一个 token 的 key 向量做点积，并对这个点积 score 做归一化（图中的 2.645 实际上是 $\sqrt7$，即 query 向量的维度 $\sqrt{d_q}$）。由此，就得到了熟悉的 $w$ 权重向量，进而执行 softmax，就得到了一个概率分布 $\alpha$ ，由此可以计算出 掘 token 的输出向量。

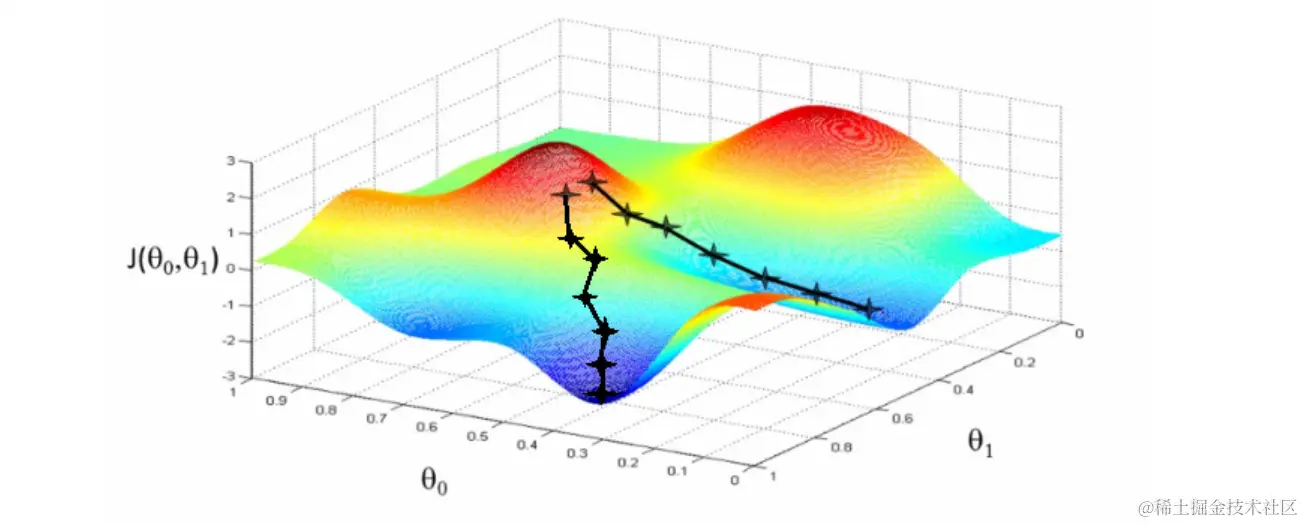
为什么要除以 $sqrt{d_q}$ ？神经网络模型的训练过程是采用梯度下降法来完成的。这里具体细节不展开，你可以参考第 8 节的内容。

梯度下降非常像一个人从山顶上走到山脚下。放在神经网络的训练中，一个良好的训练过程，是人能够顺利找到下山的路，平稳下来。而若遇到一段很长的平路，没有向下的坡路，则说明模型训练遇到了阻碍。

img

既然模型需要做梯度下降，则必须保证模型在做参数运算过程中，梯度值是存在且较大的。而 softmax 函数很容易造成梯度消失，消失原因在于，输入 softmax 函数的值过大。

在上述例子中，**$q_i k_i$ 乘积过大，会导致模型训练过程中的梯度消失，进而模型训练失败**。因此，为了限制这个乘积值，需要除以这两个向量的维度根号值，确保数值在稳定的范围内。

计算后续每个 token 位置的输出向量均同理。若想计算最后一个输出位（即空格处，第 15 个 token 要填的字）的向量，计算方法也和上面同理。

上述计算方式是一步一步地以向量表示形式展开的。若以矩阵形式做公式计算，则可以表示为：
$$
Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_q}})V
$$
其中：

  • $Q=(q_1,q_2,\ldots,q_i,\ldots,q_{d_q})$
  • $K=(k_1,k_2,\ldots,k_i,\ldots,k_{d_k})$
  • $V=(v_1,v_2,\ldots,v_i,\ldots,v_{d_v})$

其中，$QK^T$ 就是点积的矩阵形式，最右侧的 $V$ 可以理解为 token embedding 组成的矩阵。$softmax(*)V$ 实际上就是前述各个 embedding 的注意力权重 $\sum_i e_i \alpha_i$ 的矩阵表示形式，$e_i$ 表示第 $i$ 个 token 的 embedding 表示，$\alpha_i$ 是注意力权重概率值。

还需要补充说明的是，我们在讲解注意力机制的计算过程中，默认了 $q_i、k_i、v_i$ 都是 token embedding 本身，在实际的模型中却并不是这样。

第 2 节中，我们提到了 ChatGPT 模型为了体现强大的模型拟合能力，具备较为高级的智能，其模型参数量是随着规模逐渐增大的。到了 ChatGPT 的基础模型 GPT3.5，模型训练的参数规模已经达到了 1750 亿。

神经网络模型之所以很容易契合模型膨胀扩张这一需求。其关键特点在于可以加参数。

在 $q_i、k_i、v_i$ 这里，也可以扩充参数，提升模型的拟合能力。

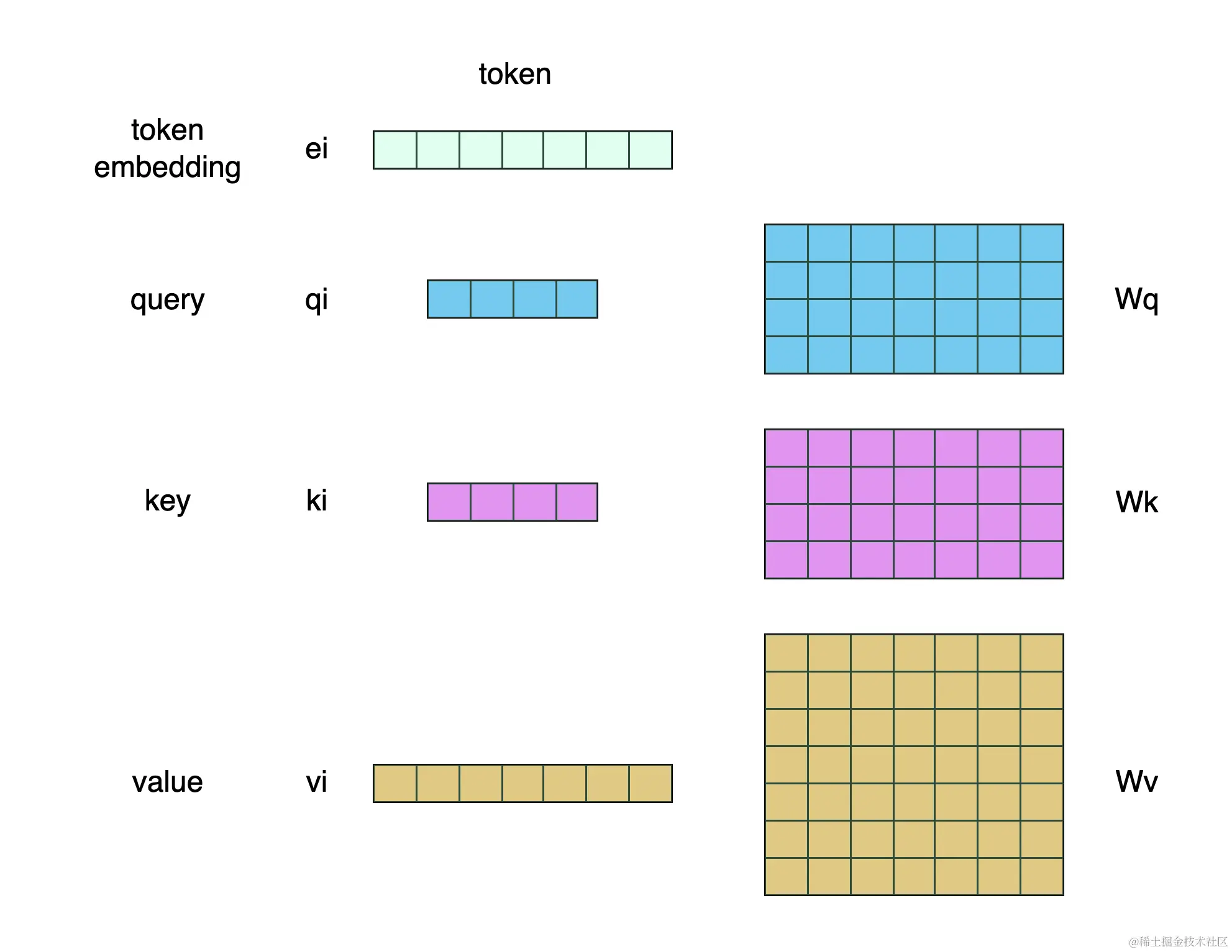
具体来讲，**$Q、K、V$ 三个模型矩阵都是由 token embedding 矩阵做一个矩阵变换得到的**。其维度也可以和 embedding 的维度不同。具体形式如下图所示。

具体过程参见「动图轻松理解 Self-Attention.md」

5-3.png

在图中，$W_Q、W_K、W_V$ 均为模型参数，它们都是神经网络模型扩展的可训练参数。其具体计算方法为：

  • $q_i=W_Q e_i$
  • $k_i=W_K e_i$
  • $v_i=W_V e_i$

需要明确的是，**$Q$ 和 $K$ 的维度必须是相同的**，这样才能保证可执行点积运算。而 $V$ 的维度则可以灵活多变，图中特意以 4 维和 7 维强调这一点。但一般来讲，三者和 token embedding 的维度保持一致即可。

如果我们把注意力机制的输入输出当作一个黑盒，我们可以观察其输入、输出为如下形式：

5-4.png

经过了一层自注意力机制之后，模型的输入和输出结构是相仿的，每一个 token 和其上下文经过对比之后，又生成了一个对应的融合了上下文信息的向量表示。

因此，我们完全可以多多堆叠自注意力层，不断地让模型学习上下文联系。ChatGPT 也确实是这么干的，这将在第 6、7 节中展开讲。

注意力机制的好处

通过本节的介绍，我们已经非常清楚，自然语言中自注意力机制是如何将每个 token 的上下文融合起来的，这是目前深度学习模型最流行的操作。

正如例句中，空格处要填写的内容，位于句子的末尾，而信息相关的 掘金 二字则位于句首，中间跨越了很多个 token，寻找两者之间的关联关系，注意力机制非常擅长。技术上讲，这叫注意力机制擅长计算长文本依赖。

而在过去，神经网络里主要使用循环神经网络（RNN）模型结构来处理。RNN 的网络结构可以使用如下公式来解释：$e_i=h(e_{i-1},W_{RNN})$。

其中，$h(*)$ 是 RNN 的计算函数，$e_i$ 是第 $i$ 个 token 的网络内的 embedding 表示，$W_{RNN}$ 是模型参数。它表示了第 $i$ 个 token 必然和其相邻的 第 $i-1$ 个 token 相关联，而无法跨 token。在处理例句的注意力时，局限性很强。

另外，深度学习中模型的计算量超级大，为了让 ChatGPT 模型能够快速输出结果，就需要采用并行计算的方式。

所谓并行计算，就是一种朴素的加速思想，一个工作，一个人干需要10天，那么找10个人来，一天时间干完。在程序里，主要就是采用多核 GPU 来计算。

注意力机制相比 RNN，更加方便模型在工程上实施并行加速计算。

总结

  • 注意力机制的本质是从大量信息中剔除杂质、无关信息，保留感兴趣的信息。
  • 注意力机制在 NLP 领域的应用主要是 自注意力 Self-Attention 形式，它是神经网络具备充分拟合能力的灵魂。
  • 在第 1 节中，我们提到了，Transformer 是构成 ChatGPT 这座房子的砖块和钢筋，而自注意力机制则是构成 Transformer 的核心要素。下一节，我们就来介绍 Transformer 结构和原理。
许可协议

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处

分享文章
✍️ Yikun Wu 已发表了 69 篇文章 · 总计 293k 字，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处

🌀 本站总访问量 次