✅ 二叉树匹配类题目总结 匹配类二叉树可以使用一种套路相对固定的递归函数,这类题目与字符串匹配有些神似,求解过程大致分为两步:
相关例题:
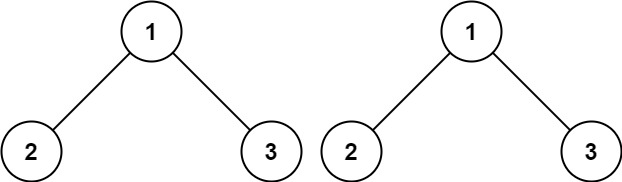
1 2 3 4 5 6 7 8 class Solution {public : bool isSameTree (TreeNode* p, TreeNode* q) if (!p || !q) return p == q; return p->val == q->val && isSameTree (p->left, q->left) && isSameTree (p->right, q->right); } };
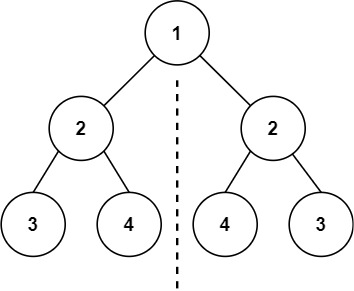
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : bool check (TreeNode* a, TreeNode* b) if (a == nullptr && b == nullptr ) return true ; if (a == nullptr || b == nullptr ) return false ; return a->val == b->val && check (a->left, b->right) && check (a->right, b->left); } bool isSymmetric (TreeNode* root) return check (root->left, root->right); } };
题意:「链表」在「二叉树」中的匹配
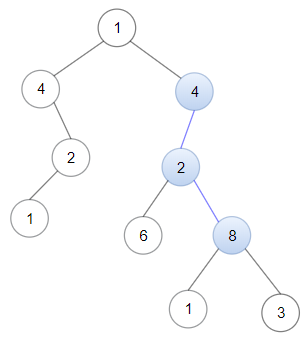
1 2 3 输入:head = [4 ,2 ,8 ], root = [1 ,4 ,4 ,null,2 ,2 ,null,1 ,null,6 ,8 ,null,null,null,null,1 ,3 ] 输出:true 解释:树中蓝色的节点构成了与链表对应的子路径。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : bool check (ListNode* head, TreeNode* root) if (head == nullptr ) return true ; if (root == nullptr ) return false ; return head->val == root->val && (check (head->next, root->left) || check (head->next, root->right)); } bool isSubPath (ListNode* head, TreeNode* root) if (root == nullptr ) return false ; return check (head, root) || isSubPath (head, root->left) || isSubPath (head, root->right); } };
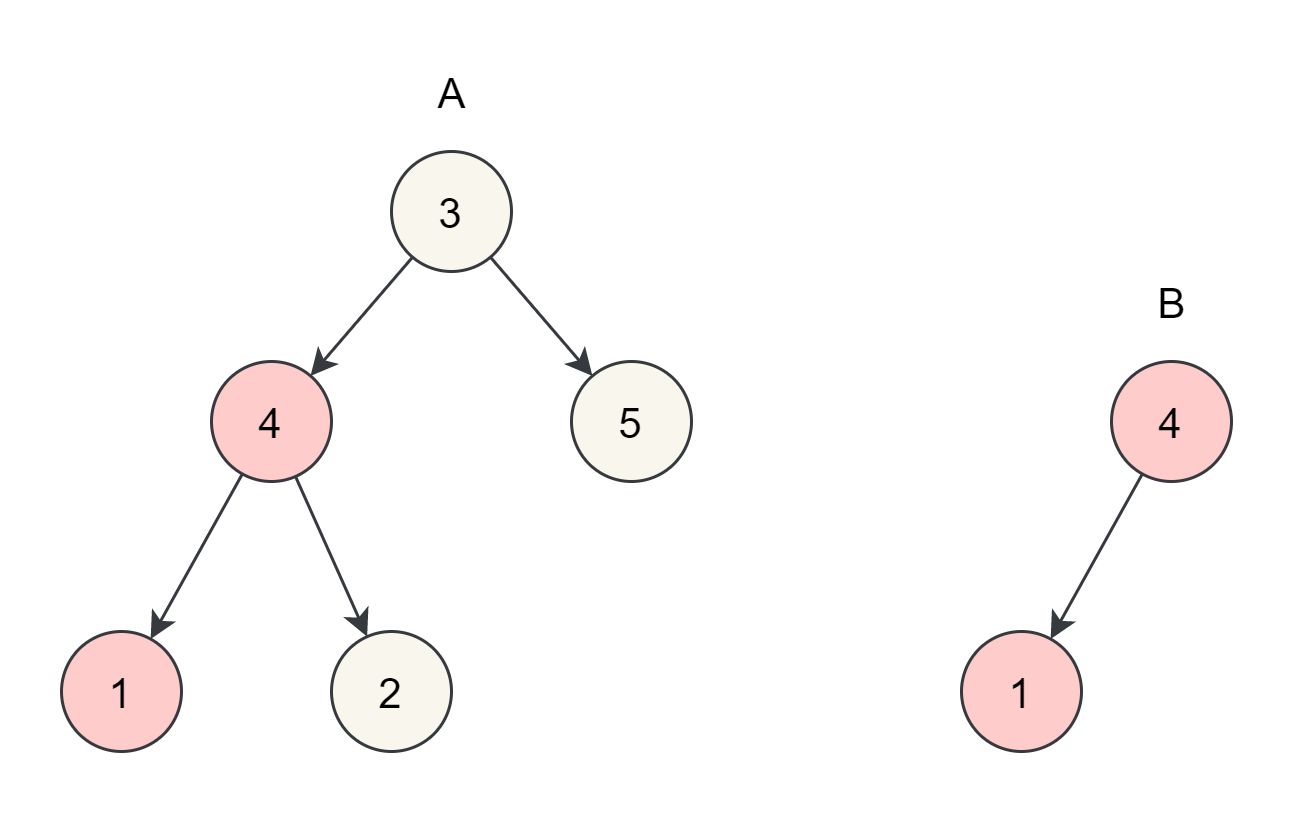
这道题的题意是这样的:输入两棵二叉树 A 和 B,判断 B 是不是 A 的子结构,且约定空树不是任意一个树的子结构。
比如上面这个例子,我们发现 B 是 A 的子结构,因为它们的结构相同,且节点值相等。
求解思路可以分解为以下两步:
匹配根节点:首先在 A 中找到与 B 的根节点匹配的节点 C;
匹配其他节点:验证 C 的子树与 B 的子树是否匹配。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : bool check (TreeNode* a, TreeNode* b) if (a == nullptr && b == nullptr ) return true ; if (a == nullptr || b == nullptr ) return false ; return a->val == b->val && check (a->left, b->left) && check (a->right, b->right); } bool checkSubTree (TreeNode* t1, TreeNode* t2) if (t1 == nullptr || t2 == nullptr ) return false ; return check (t1, t2) || checkSubTree (t1->left, t2) || checkSubTree (t1->right, t2); } };
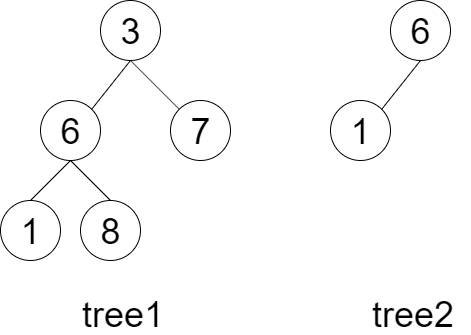
1 2 3 输入:tree1 = [3 ,6 ,7 ,1 ,8 ], tree2 = [6 ,1 ] 输出:true 解释:tree2 与 tree1 的一个子树拥有相同的结构和节点值。即 6 - > 1 。
对于本题来讲,与「面试题 04.10. 检查子树」很像,不同的是 B 属于 A 的一部分也可以,没必要一直匹配到叶子节点,因此只需对 check 函树的基本条件进行修改即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : bool check (TreeNode* a, TreeNode* b) if (b == nullptr ) return true ; if (a == nullptr ) return false ; return a->val == b->val && check (a->left, b->left) && check (a->right, b->right); } bool isSubStructure (TreeNode* t1, TreeNode* t2) if (t1 == nullptr || t2 == nullptr ) return false ; return check (t1, t2) || isSubStructure (t1->left, t2) || isSubStructure (t1->right, t2); } };