✅ 优先队列 priority_queue

更多关于优先队列的知识，请跳转至：https://en.oi-wiki.org/lang/pb-ds/pq/

  • 大顶堆：priority_queue<int> pq

  • 小顶堆：priority_queue<int, vector<int>, greater<>> pq

相关例题：

__gnu_pbds :: priority_queue

附： 官方文档地址——复杂度及常数测试

1
2
3
#include <ext/pb_ds/priority_queue.hpp>
using namespace __gnu_pbds;
__gnu_pbds ::priority_queue<T, Compare, Tag, Allocator>

模板形参：

  • T : 储存的元素类型
  • Compare : 提供严格的弱序比较类型
  • Tag 是 __gnu_pbds 提供的不同的五种堆，Tag 参数默认是 pairing_heap_tag，这五种分别是：
    • pairing_heap_tag ：配对堆，官方文档认为在非原生元素（如自定义结构体/ std :: string / pair ) 中，配对堆表现最好
    • binary_heap_tag ：二叉堆，官方文档认为在原生元素中二叉堆表现最好，不过我测试的表现并没有那么好
    • binomial_heap_tag ：二项堆，二项堆在合并操作的表现要优于配对堆*但是其取堆顶元素的
    • rc_binomial_heap_tag ：冗余计数二项堆
    • thin_heap_tag ：除了合并的复杂度都和 Fibonacci 堆一样的一个 tag
  • Allocator ：空间配置器，由于 OI 中很少出现，故这里不做讲解

由于本篇文章只是提供给学习算法竞赛的同学们，故对于后四个 tag 只会简单的介绍复杂度，第一个会介绍成员函数和使用方法。

经作者本机测试堆的基础操作，结合 GNU 官方的复杂度测试，Dijkstra 测试，都表明：至少对于 OIer 来讲，除了配对堆（即默认 tag）的其他四个 tag 都是鸡肋，要么没用，要么常数大到不如 std 的，且有可能造成 MLE，故这里只推荐用默认的配对堆。同样，配对堆也优于 algorithm 库中的 make_heap() 。

构造方式

要注明命名空间因为和 std 的类名称重复。

1
2
3
4
5
__gnu_pbds ::priority_queue<int> __gnu_pbds::priority_queue<int, greater<int> >
__gnu_pbds ::priority_queue<int, greater<int>, pairing_heap_tag>
__gnu_pbds ::priority_queue<int>::point_iterator id; // 迭代器
// 在 modify 和 push 的时候都会返回一个 point_iterator，下文会详细的讲使用方法
id = q.push(1);

成员函数

  • push() : 向堆中压入一个元素，返回该元素位置的迭代器。
  • pop() : 将堆顶元素弹出。
  • top() : 返回堆顶元素。
  • size() 返回元素个数。
  • empty() 返回是否非空。
  • modify(point_iterator, const key) : 把迭代器位置的 key 修改为传入的 key ，并对底层储存结构进行排序。
  • erase(point_iterator) : 把迭代器位置的键值从堆中擦除。
  • join(__gnu_pbds :: priority_queue &other) : 把 other 合并到 *this 并把 other 清空。

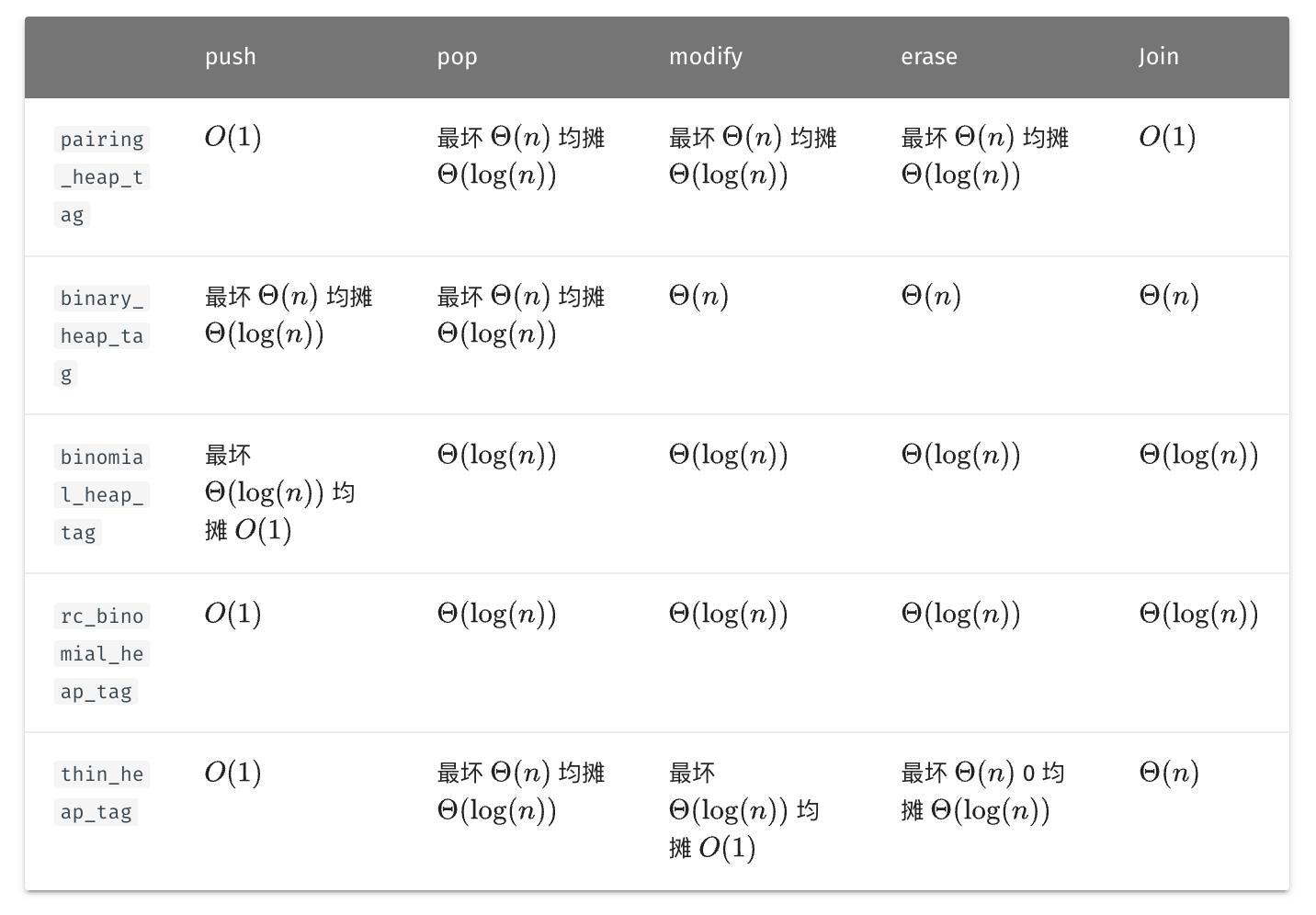
时间复杂度

使用的 tag 决定了每个操作的时间复杂度：

239. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

1
2
3
4
5
6
7
8
9
10
11
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        // entry: <val, idx (whether_expired)>
        priority_queue<pair<int, int>, vector<pair<int, int>>, less<>> pq;
        for (int i = 0; i < k; i++) {
            pq.emplace(nums[i], i);
        }
        vector<int> ans{pq.top().first};
        for (int i = k; i < nums.size(); i++) {
            pq.emplace(nums[i], i);
            while (pq.top().second <= i - k) {
                pq.pop();
            }
            ans.push_back(pq.top().first);
        }
        return ans;
    }
};

295. 数据流的中位数

中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。

  • 例如 arr = [2,3,4] 的中位数是 3 。
  • 例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。

实现 MedianFinder 类:

  • MedianFinder() 初始化 MedianFinder 对象。
  • void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
  • double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。
1
2
3
4
5
6
7
8
9
10
11
12
13
输入
["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"]
[[], [1], [2], [], [3], []]
输出
[null, null, null, 1.5, null, 2.0]

解释
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1);    // arr = [1]
medianFinder.addNum(2);    // arr = [1, 2]
medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2)
medianFinder.addNum(3);    // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class MedianFinder {
private:
    priority_queue<int> left;                          // 大顶堆
    priority_queue<int, vector<int>, greater<>> right; // 小顶堆

public:
    MedianFinder() {}

    void addNum(int num) {
        // 分类讨论, 并且合并为最终两种情况
        if (left.size() == right.size()) {
            right.push(num);
            left.push(right.top());
            right.pop();
        } else {
            left.push(num);
            right.push(left.top());
            left.pop();
        }
    }

    double findMedian() {
        return (left.size() + right.size()) % 2
                   ? left.top()
                   : static_cast<double>(left.top() + right.top()) / 2;
    }
};

480. 滑动窗口中位数

中位数是有序序列最中间的那个数。如果序列的长度是偶数，则没有最中间的数；此时中位数是最中间的两个数的平均数。

例如：

  • [2,3,4]，中位数是 3
  • [2,3]，中位数是 (2 + 3) / 2 = 2.5

给你一个数组 nums，有一个长度为 k 的窗口从最左端滑动到最右端。窗口中有 k 个数，每次窗口向右移动 1 位。你的任务是找出每次窗口移动后得到的新窗口中元素的中位数，并输出由它们组成的数组。

给出 nums = [1,3,-1,-3,5,3,6,7]，以及 k = 3。

1
2
3
4
5
6
7
8
窗口位置                      中位数
---------------               -----
[1  3  -1] -3  5  3  6  7       1
 1 [3  -1  -3] 5  3  6  7      -1
 1  3 [-1  -3  5] 3  6  7      -1
 1  3  -1 [-3  5  3] 6  7       3
 1  3  -1  -3 [5  3  6] 7       5
 1  3  -1  -3  5 [3  6  7]      6

因此，返回该滑动窗口的中位数数组 [1,-1,-1,3,5,6]。

1️⃣ 哈希表 + 逻辑删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class Solution {
public:
    priority_queue<int> left;                          // 滑动窗口中左半部分
    priority_queue<int, vector<int>, greater<>> right; // 滑动窗口中右半部分
    unordered_map<int, int> mp;                        // 用于逻辑删除

    double get(int k) {
        if (k % 2)
            return left.top();
        else
            return ((long long)left.top() + right.top()) / 2.0;
    }

    vector<double> medianSlidingWindow(vector<int>& nums, int k) {
        for (int i = 0; i < k; i++) {
            int x = nums[i];
            if (left.size() == right.size()) {
                right.push(x);
                left.push(right.top());
                right.pop();
            } else {
                left.push(x);
                right.push(left.top());
                left.pop();
            }
        }
        vector<double> ans{get(k)};

        for (int i = k; i < nums.size(); i++) {
            int balance = 0; // right.size() - left.size()

            // [fake] delete
            int l_num = nums[i - k];
            mp[l_num]++;
            if (!left.empty() && l_num <= left.top()) {
                balance++;
            } else {
                balance--;
            }

            // add
            if (!left.empty() && nums[i] <= left.top()) {
                left.push(nums[i]);
                balance--;
            } else {
                right.push(nums[i]);
                balance++;
            }

            // adjust
            if (balance > 0) {
                left.push(right.top());
                right.pop();
            } else if (balance < 0) {
                right.push(left.top());
                left.pop();
            }

            // delete
            while (!left.empty() && mp[left.top()] > 0) {
                mp[left.top()]--;
                left.pop();
            }
            while (!right.empty() && mp[right.top()] > 0) {
                mp[right.top()]--;
                right.pop();
            }

            ans.push_back(get(k));
        }
        return ans;
    }
}

2️⃣ 懒删除堆

本题等价于：295. 数据流的中位数 + 懒删除堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
template<typename T, typename Compare = less<T>>
class LazyHeap {
    priority_queue<T, vector<T>, Compare> pq;
    unordered_map<T, int> remove_cnt; // 每个元素剩余需要删除的次数
    size_t sz = 0; // 实际大小

    // 正式执行删除操作
    void apply_remove() {
        while (!pq.empty() && remove_cnt[pq.top()] > 0) {
            remove_cnt[pq.top()]--;
            pq.pop();
        }
    }

public:
    size_t size() {
        return sz;
    }

    // 删除
    void remove(T x) {
        remove_cnt[x]++; // 懒删除
        sz--;
    }

    // 查看堆顶
    T top() {
        apply_remove();
        return pq.top();
    }

    // 出堆
    T pop() {
        apply_remove();
        sz--;
        T x = pq.top();
        pq.pop();
        return x;
    }

    // 入堆
    void push(T x) {
        if (remove_cnt[x] > 0) {
            remove_cnt[x]--; // 抵消之前的删除
        } else {
            pq.push(x);
        }
        sz++;
    }

    // push(x) 然后 pop()
    T push_pop(T x) {
        apply_remove();
        pq.push(x);
        x = pq.top();
        pq.pop();
        return x;
    }
};

class Solution {
public:
    vector<double> medianSlidingWindow(vector<int>& nums, int k) {
        int n = nums.size();
        vector<double> ans(n - k + 1);
        LazyHeap<int> left; // 最大堆
        LazyHeap<int, greater<int>> right; // 最小堆

        for (int i = 0; i < n; i++) {
            // 1. 进入窗口
            int in = nums[i];
            if (left.size() == right.size()) {
                left.push(right.push_pop(in));
            } else {
                right.push(left.push_pop(in));
            }

            int l = i + 1 - k;
            if (l < 0) { // 窗口大小不足 k
                continue;
            }

            // 2. 计算答案
            if (k % 2) {
                ans[l] = left.top();
            } else {
                ans[l] = ((long long) left.top() + right.top()) / 2.0;
            }

            // 3. 离开窗口
            int out = nums[l];
            if (out <= left.top()) {
                left.remove(out);
                if (left.size() < right.size()) {
                    left.push(right.pop()); // 平衡两个堆的大小
                }
            } else {
                right.remove(out);
                if (left.size() > right.size() + 1) {
                    right.push(left.pop()); // 平衡两个堆的大小
                }
            }
        }

        return ans;
    }
};
License

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。

Share

Join discussion～

本站总访问量 次

本站共发表 112 篇文章 · 总计 389.5k 字
载入天数...载入时分秒...