这是一种经常考察的思维「大数相加」题型

这是一种经常考察的思维：大数相加。一般有以下几种数据结构类型的考察方式：

66. 加一 ｜数组版

给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

1
2
3
输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
        int n = digits.size(), add = 1;
        for (int i = n - 1; i >= 0 && add; i--) {
            int res = digits[i] + 1;
            digits[i] = res % 10;
            add = res / 10;
        }
        if (add) {
            digits.insert(digits.begin(), 1);
        }
        return digits;
    }
};

415. 字符串相加 ｜字符串版

给定两个字符串形式的非负整数 num1 和num2 ，计算它们的和并同样以字符串形式返回。

你不能使用任何內建的用于处理大整数的库（比如 BigInteger）， 也不能直接将输入的字符串转换为整数形式。

示例 1：

1
2
输入：num1 = "11", num2 = "123"
输出："134"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    string addStrings(string num1, string num2) {
        int i = num1.length() - 1, j = num2.length() - 1, add = 0;
        string ans = "";
        while (i >= 0 || j >= 0 || add) {
            int x = i >= 0 ? num1[i] - '0' : 0;
            int y = j >= 0 ? num2[j] - '0' : 0;
            int result = x + y + add;
            ans.push_back('0' + result % 10);
            add = result / 10;
            i--;
            j--;
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

2. 两数相加 ｜链表版 · 从头开始➕

img

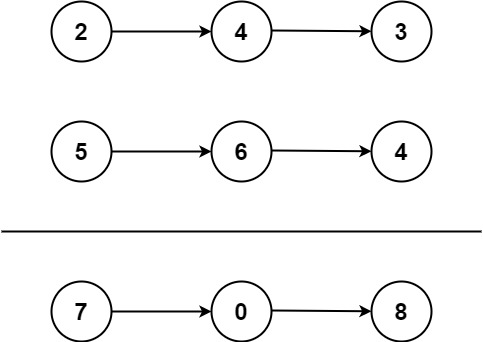
1
2
3
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.
1
2
输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

1️⃣ 迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode dummy;
        ListNode* cur = &dummy;
        int carry = 0;
        while (l1 || l2 || carry) {
            int res = 0;
            if (l1) {
                res += l1->val;
                l1 = l1->next;
            }
            if (l2) {
                res += l2->val;
                l2 = l2->next;
            }
            res += carry;
            carry = res / 10;
            cur = cur->next = new ListNode(res % 10);
        }
        return dummy.next;
    }
};

2️⃣ 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2, int carry = 0) {
        if (!l1 && !l2) {
            return carry ? new ListNode(carry) : nullptr;
        }
        if (!l1) {
            swap(l1, l2);
        }
        int sum = carry + l1->val + (l2 ? l2->val : 0);
        l1->val = sum % 10;
        l1->next = addTwoNumbers(l1->next, (l2 ? l2->next : nullptr), sum / 10);
        return l1;
    }
};

445. 两数相加 II ｜链表版 · 从尾开始➕

img

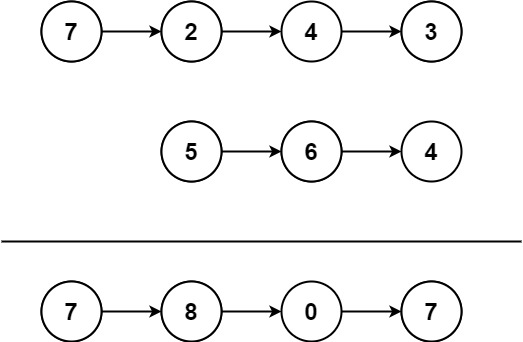
1
2
输入：l1 = [7,2,4,3], l2 = [5,6,4]
输出：[7,8,0,7]

✅ 两数相加 II = 两数相加 + 反转链表

1️⃣ 迭代｜206. 反转链表（迭代）+ 2. 两数相加（迭代）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2);
        ListNode dummy;
        ListNode* cur = &dummy;
        int carry = 0;
        while (l1 || l2 || carry) {
            int res = carry;
            if (l1) {
                res += l1->val;
                l1 = l1->next;
            }
            if (l2) {
                res += l2->val;
                l2 = l2->next;
            }
            carry = res / 10;
            cur = cur->next = new ListNode(res % 10);
        }
        return reverseList(dummy.next);
    }
};

2️⃣ 递归｜206. 反转链表（递归）+ 2. 两数相加（递归）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        ListNode* new_head = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return new_head;
    }

    ListNode* addTwo(ListNode* l1, ListNode* l2, int carry = 0) {
        if (!l1 && !l2) {
            return carry ? new ListNode(carry) : nullptr;
        }
        if (!l1) {
            swap(l1, l2);
        }
        int sum = carry + l1->val + (l2 ? l2->val : 0);
        l1->val = sum % 10;
        l1->next = addTwo(l1->next, (l2 ? l2->next : nullptr), sum / 10);
        return l1;
    }

    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2);
        ListNode* head = addTwo(l1, l2, 0);
        return reverseList(head);
    }
};

67. 二进制求和 ｜二进制版

给你两个二进制字符串 a 和 b ，以二进制字符串的形式返回它们的和。

示例 1：

1
2
输入:a = "11", b = "1"
输出："100"

示例 2：

1
2
输入：a = "1010", b = "1011"
输出："10101"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    string addBinary(string a, string b) {
        int carry = 0;
        int i = a.length() - 1, j = b.length() - 1;
        string ans;
        while (i >= 0 || j >= 0 || carry) {
            int x = i >= 0 ? a[i--] - '0' : 0;
            int y = j >= 0 ? b[j--] - '0' : 0;
            int s = x + y + carry;
            carry = s / 2;
            ans.push_back(s % 2 + '0');
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

43. 字符串相乘 ｜大数相乘✖️

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

注意：不能使用任何内置的 Big Integer 库或直接将输入转换为整数。

示例 1:

1
2
输入: num1 = "2", num2 = "3"
输出: "6"

示例 2:

1
2
输入: num1 = "123", num2 = "456"
输出: "56088"

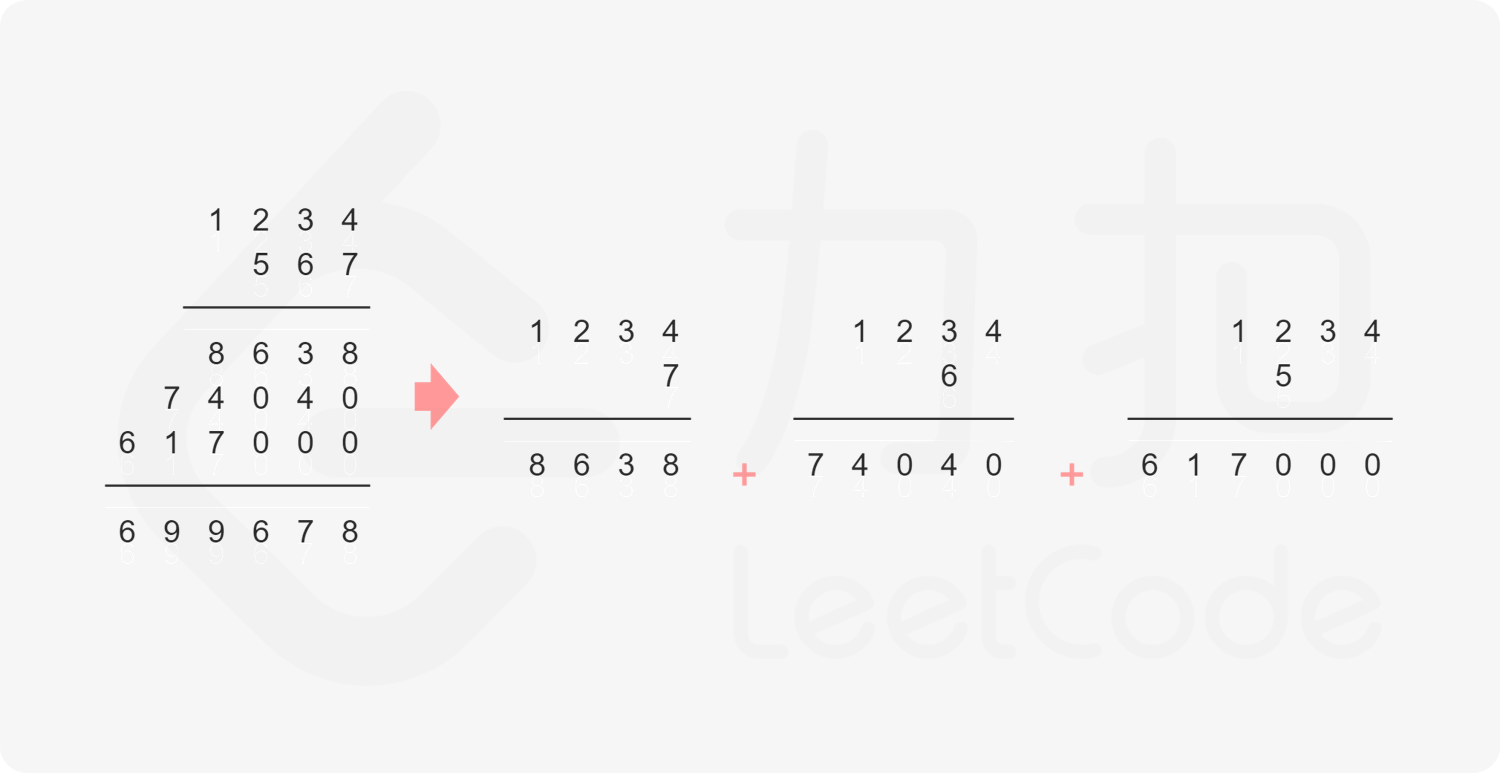
1️⃣ 竖式相加

思路：建立在「大数相加」的基础上，因为多个数之间需要累加（容易理解）

fig1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
public:
    // 大数相加
    string addStrings(string num1, string num2) {
        int i = num1.length() - 1, j = num2.length() - 1, add = 0;
        string ans = "";
        while (i >= 0 || j >= 0 || add) {
            int x = i >= 0 ? num1[i] - '0' : 0;
            int y = j >= 0 ? num2[j] - '0' : 0;
            int result = x + y + add;
            add = result / 10;
            ans.push_back('0' + result % 10);
            i--;
            j--;
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }

    // 大数相乘
    string multiply(string num1, string num2) {
        if (num1 == "0" || num2 == "0")
            return "0";
        int multiply = 0;
        int m = num1.length(), n = num2.length();
        string ans = "0";
        for (int i = m - 1; i >= 0; i--) {
            int x = num1[i] - '0';
            string num;
            int add = 0;
            for (int j = n - 1; j >= 0 || add; j--) {
                if (x == 0) {
                    num = "0";
                    break;
                }
                if (j < 0) {
                    num.push_back('0' + add);
                    break;
                }
                int y = num2[j] - '0';
                int result = x * y + add;
                add = result / 10;
                num.push_back('0' + result % 10);
            }
            reverse(num.begin(), num.end());
            if (num != "0")
                ans = addStrings(ans, num + string(multiply, '0'));
            multiply++;
        }
        return ans;
    }
};

2️⃣ 相乘

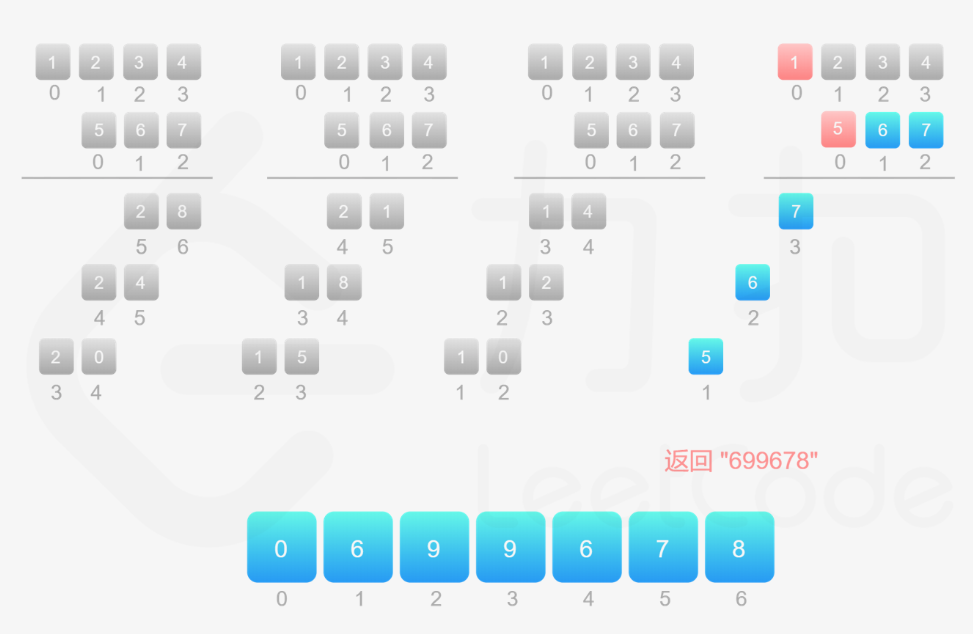
思路：直接做乘法，长度分别为 m 和 n 的数字相乘，值长度不超过 m + n，vector<int> ansArr(m + n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    string multiply(string num1, string num2) {
        if (num1 == "0" || num2 == "0") {
            return "0";
        }
        int m = num1.length(), n = num2.length();
        vector<int> ansArr(m + n);
        for (int i = m - 1; i >= 0; i--) {
            int x = num1[i] - '0';
            for (int j = n - 1; j >= 0; j--) {
                int y = num2[j] - '0';
                ansArr[i + j + 1] += x * y;
            }
        }
        for (int i = m + n - 1; i > 0; i--) {
            ansArr[i - 1] += ansArr[i] / 10;
            ansArr[i] %= 10;
        }
        int idx = ansArr[0] == 0 ? 1 : 0;
        string ans;
        while (idx < m + n) {
            ans.push_back('0' + ansArr[idx]);
            idx++;
        }
        return ans;
    }
};
许可协议

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处

分享文章
✍️ Yikun Wu 已发表了 69 篇文章 · 总计 293k 字，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处

🌀 本站总访问量 次