高频「链表」面试题

面试经常考察链表题型！

✅ 高频链表面试题

141. 环形链表

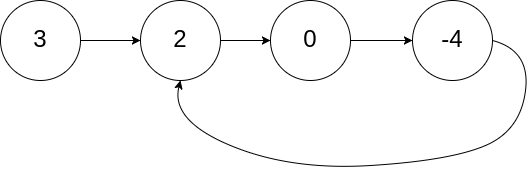
1
2
3

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

1️⃣ 快慢指针

class Solution {
public:
    bool hasCycle(ListNode* head) {
        ListNode *slow = head, *fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast)
                return true;
        }
        return false;
    }
};

142. 环形链表 II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

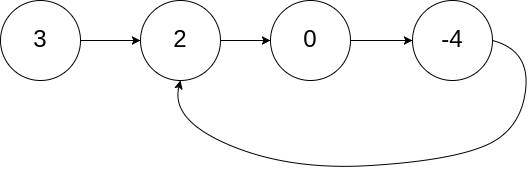
1
2
3

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

1️⃣ 快慢指针

fig1

class Solution {
public:
    ListNode* detectCycle(ListNode* head) {
        ListNode *slow = head, *fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) {
                // a = k(b + c) + c
                ListNode* node = head;
                while (node != slow) {
                    node = node->next;
                    slow = slow->next;
                }
                return slow;
            }
        }
        return nullptr;
    }
};

160. 相交链表

class Solution {
public:
    ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
        ListNode *p = headA, *q = headB;
        while (p != q) {
            p = p ? p->next : headB;
            q = q ? q->next : headA;
        }
        return p;
    }
};

206. 反转链表

1️⃣ 迭代｜三指针

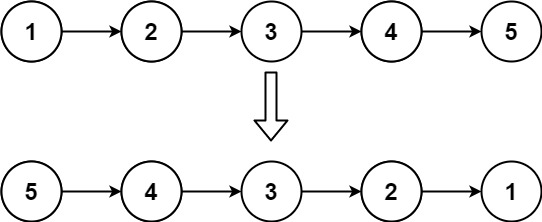
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }
};

2️⃣ 递归

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next)
            return head;
        ListNode* new_head = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;   // 为了反转后的末节点
        return new_head;
    }
};

92. 反转链表 II

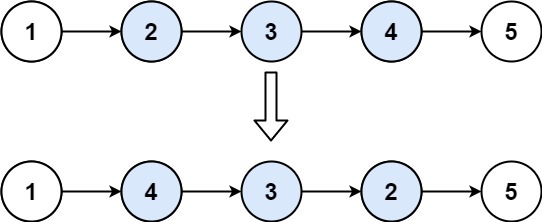
反转链表进阶：反转部分区间，找到区间 leftNode 与 rightNode，以及 leftNode 左节点 pre 与 rightNode 右节点 nxt，独立区间（断开连接）后反转再接回。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode dummy(0, head);
        ListNode* pre = &dummy;
        int t = left;
        while (--t) {
            pre = pre->next;
        }
        ListNode* leftNode = pre->next;
        ListNode* rightNode = leftNode;
        t = right - left;
        while (t--) {
            rightNode = rightNode->next;
        }
        ListNode* nxt = rightNode->next;
        // 断开链接
        pre->next = nullptr;
        rightNode->next = nullptr;
        // 反转链表
        ListNode* node = reverseList(leftNode);
        // 重新链接
        pre->next = node;
        leftNode->next = nxt;
        return dummy.next;
    }
};

876. 链表的中间结点

1
2
3

输入：head = [1,2,3,4,5]
输出：[3,4,5]
解释：链表只有一个中间结点，值为 3 。

1
2
3

输入：head = [1,2,3,4,5,6]
输出：[4,5,6]
解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。

1️⃣ 快慢指针

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode *slow = head, *fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }
};

234. 回文链表

1️⃣ 回文链表判断 = 寻找中间节点 + 反转链表

前置题目：

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode *slow = head, *fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }

    ListNode* reverseList(ListNode* head) {
        ListNode *pre = nullptr, *cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    bool isPalindrome(ListNode* head) {
        ListNode* mid = middleNode(head);
        ListNode* head2 = reverseList(mid);
        while (head2) {
            if (head->val != head2->val) {
                return false;
            }
            head = head->next;
            head2 = head2->next;
        }
        return true;
    }
};

21. 合并两个有序链表

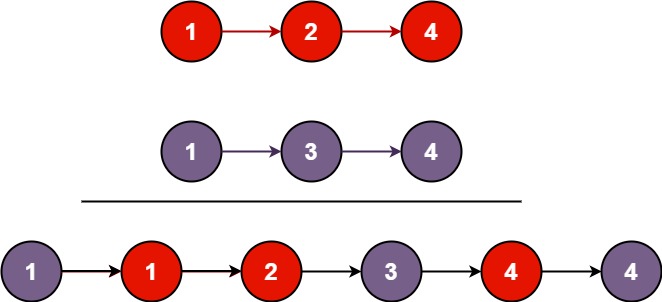
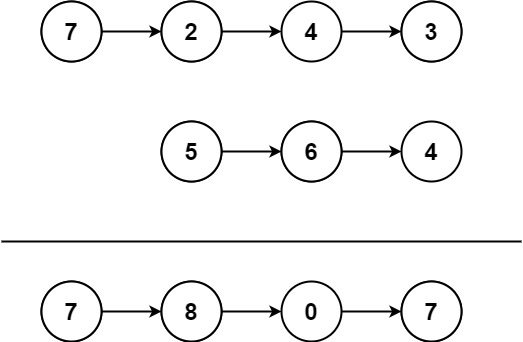
1 2	输入：l1 = [1,2,4], l2 = [1,3,4] 输出：[1,1,2,3,4,4]

1️⃣ 迭代（常用）

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode dummy{};
        ListNode* cur = &dummy;
        while (list1 && list2) {
            if (list1->val < list2->val) {
                cur->next = list1;
                list1 = list1->next;
            } else {
                cur->next = list2;
                list2 = list2->next;
            }
            cur = cur->next;
        }
        cur->next = list1 ? list1 : list2;
        return dummy.next;
    }
};

2️⃣ 递归

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if (list1 == nullptr) return list2; // 注：如果都为空则返回空
        if (list2 == nullptr) return list1;
        if (list1->val < list2->val) {
            list1->next = mergeTwoLists(list1->next, list2);
            return list1;
        }
        list2->next = mergeTwoLists(list1, list2->next);
        return list2;
    }
};

2. 两数相加｜从头开始相加

1️⃣ 迭代

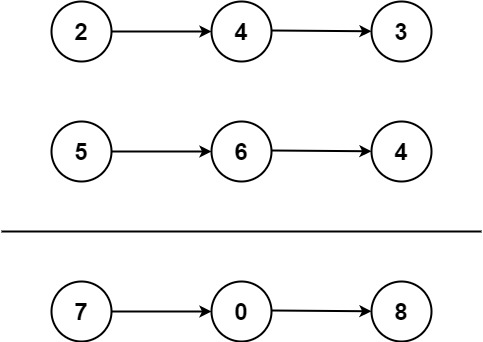
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode dummy;
        ListNode* cur = &dummy;
        int carry = 0;
        while (l1 || l2 || carry) {
            if (l1) {
                carry += l1->val;
                l1 = l1->next;
            }
            if (l2) {
                carry += l2->val;
                l2 = l2->next;
            }
            cur = cur->next = new ListNode(carry % 10);
            carry /= 10;
        }
        return dummy.next;
    }
};

2️⃣ 递归

class Solution {
public:
    // l1 和 l2 为当前遍历的节点，carry 为进位
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2, int carry = 0) {
        if (l1 == nullptr && l2 == nullptr) { // 递归边界：l1 和 l2 都是空节点
            return carry ? new ListNode(carry) : nullptr; // 如果进位了，就额外创建一个节点
        }
        if (l1 == nullptr) { // 如果 l1 是空的，那么此时 l2 一定不是空节点
            swap(l1, l2); // 交换 l1 与 l2，保证 l1 非空，从而简化代码
        }
        int sum = carry + l1->val + (l2 ? l2->val : 0); // 节点值和进位加在一起
        l1->val = sum % 10; // 每个节点保存一个数位（直接修改原链表）
        l1->next = addTwoNumbers(l1->next, (l2 ? l2->next : nullptr), sum / 10); // 进位
        return l1;
    }
};

445. 两数相加 II ｜从尾开始相加

1️⃣ 迭代｜反转链表 + 两数相加

class Solution {
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr, *cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    ListNode* addTwo(ListNode* l1, ListNode* l2) {
        ListNode dummy; // 哨兵节点
        auto cur = &dummy;
        int carry = 0; // 进位
        while (l1 || l2 || carry) { // 有一个不是空节点，或者还有进位，就继续迭代
            if (l1) carry += l1->val; // 节点值和进位加在一起
            if (l2) carry += l2->val; // 节点值和进位加在一起
            cur = cur->next = new ListNode(carry % 10); // 每个节点保存一个数位
            carry /= 10; // 新的进位
            if (l1) l1 = l1->next; // 下一个节点
            if (l2) l2 = l2->next; // 下一个节点
        }
        return dummy.next; // 哨兵节点的下一个节点就是头节点
    }

public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2);
        auto l3 = addTwo(l1, l2);
        return reverseList(l3);
    }
};

2️⃣ 递归｜反转链表 + 两数相加

class Solution {
    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        auto new_head = reverseList(head->next);
        head->next->next = head; // 把下一个节点指向自己
        head->next = nullptr; // 断开指向下一个节点的连接，保证最终链表的末尾节点的 next 是空节点
        return new_head;
    }

    // l1 和 l2 为当前遍历的节点，carry 为进位
    ListNode* addTwo(ListNode* l1, ListNode* l2, int carry = 0) {
        if (l1 == nullptr && l2 == nullptr) { // 递归边界：l1 和 l2 都是空节点
            return carry ? new ListNode(carry) : nullptr; // 如果进位了，就额外创建一个节点
        }
        if (l1 == nullptr) { // 如果 l1 是空的，那么此时 l2 一定不是空节点
            swap(l1, l2); // 交换 l1 与 l2，保证 l1 非空，从而简化代码
        }
        carry += l1->val + (l2 ? l2->val : 0); // 节点值和进位加在一起
        l1->val = carry % 10; // 每个节点保存一个数位
        l1->next = addTwo(l1->next, (l2 ? l2->next : nullptr), carry / 10); // 进位
        return l1;
    }

public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2); // l1 和 l2 反转后，就变成【2. 两数相加】了
        auto l3 = addTwo(l1, l2);
        return reverseList(l3);
    }
};

19. 删除链表的倒数第 N 个结点

1️⃣ 快慢指针

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode dummy(0, head);
        ListNode *fast = &dummy, *slow = &dummy;
        while (n--) {
            fast = fast->next;
        }
        while (fast->next) {
            slow = slow->next;
            fast = fast->next;
        }
        ListNode* d = slow->next;
        slow->next = d->next;
        delete d;
        return dummy.next;
    }
};

24. 两两交换链表中的节点

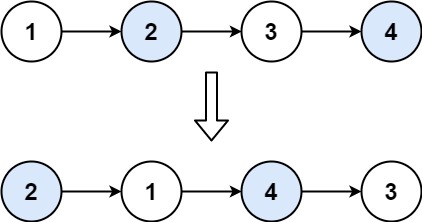
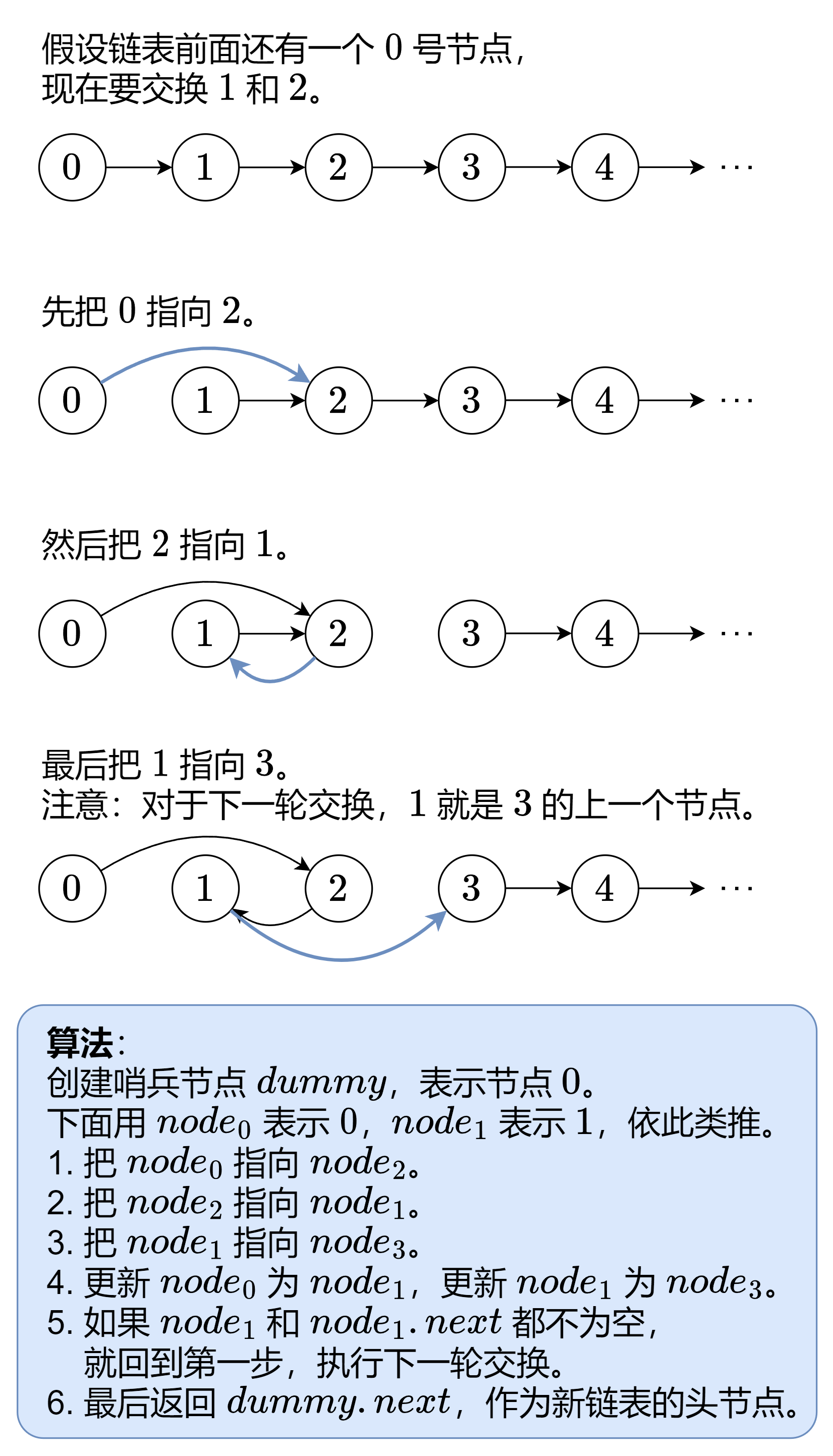
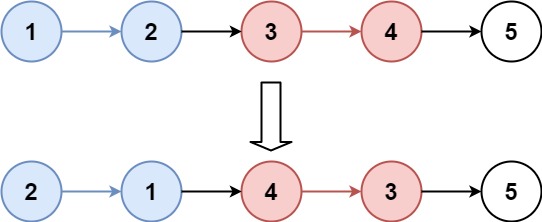
1️⃣ 迭代｜四指针

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode dummy(0, head); // 用哨兵节点简化代码逻辑
        ListNode* node0 = &dummy;
        ListNode* node1 = head;
        while (node1 && node1->next) { // 至少有两个节点
            ListNode* node2 = node1->next;
            ListNode* node3 = node2->next;

            node0->next = node2; // 0 -> 2
            node2->next = node1; // 2 -> 1
            node1->next = node3; // 1 -> 3

            node0 = node1; // 下一轮交换，0 是 1
            node1 = node3; // 下一轮交换，1 是 3
        }
        return dummy.next; // 返回新链表的头节点
    }
};

2️⃣ 递归

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }

        ListNode* node1 = head;
        ListNode* node2 = head->next;
        ListNode* node3 = node2->next;

        node1->next = swapPairs(node3); // 1 指向递归返回的链表头
        node2->next = node1; // 2 指向 1

        return node2; // 返回交换后的链表头节点
    }
};

25. K 个一组翻转链表

1️⃣ 从「反转链表 · 迭代版」到「K 个一组翻转链表」

class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        int n = 0;
        for (ListNode* cur = head; cur; cur = cur->next) {
            n++;
        }
        ListNode dummy(0, head);
        ListNode* p0 = &dummy;
        ListNode* prev = nullptr;
        ListNode* cur = head;
        for (; n >= k; n -= k) {
            for (int i = 0; i < k; i++) {
                ListNode* nxt = cur->next;
                cur->next = prev;
                prev = cur;
                cur = nxt;
            }
            ListNode* last = p0->next;
            p0->next = prev;
            last->next = cur;
            p0 = last;
        }
        return dummy.next;
    }
};

2️⃣「206. 反转链表」+「92. 反转链表 II」

class Solution {
public:
    // 206. 反转链表
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    // 92. 反转链表 II
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode dummy(0, head);
        ListNode* pre = &dummy;
        for (int i = 0; i < left - 1; i++) {
            pre = pre->next;
        }
        ListNode* leftNode = pre->next;
        ListNode* rightNode = leftNode;
        for (int i = left; i < right; i++) {
            rightNode = rightNode->next;
        }
        ListNode* nxt = rightNode->next;
        rightNode->next = nullptr;
        reverseList(leftNode);
        pre->next = rightNode;
        leftNode->next = nxt;
        return dummy.next;
    }

    ListNode* reverseKGroup(ListNode* head, int k) {
        int n = 0;
        ListNode* cur = head;
        while (cur) {
            n++;
            cur = cur->next;
        }
        if (n < k) {
            return head;
        }
        ListNode* new_head = head;
        int times = n / k;
        for (int i = 0; times--; i += k) {
            ListNode* node = reverseBetween(new_head, i + 1, i + k);
            if (i == 0) {
                new_head = node;
            }
        }
        return new_head;
    }
};

23. 合并 K 个升序链表

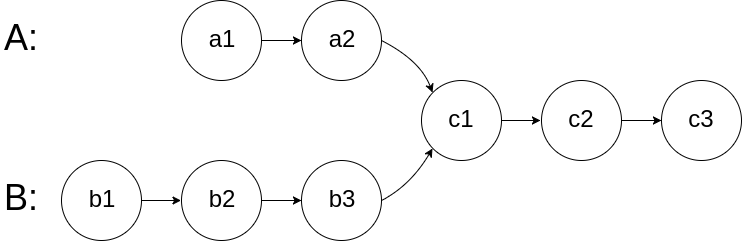
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

✅ 快手一面，面试官来一题简单题😊，最后还问了时间复杂度：假设 k 个链表，共 n 个节点，那时间复杂度为 $O(k·logk+n·logk)$ 即 $O(n·logk)$。

1️⃣ 最小堆

时间复杂度分析：假设 $k$ 个链表, 共 $n$ 个节点, 最小堆单次操作 $O(log k)$, 初始化堆需要 $O(k·logk)$, 那时间复杂度为 $O(k·logk + n·logk)$，即 $O(n·logk)$。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        auto cmp = [](const ListNode* a, const ListNode* b) {
            return a->val > b->val;
        };
        priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq;
        for (auto& head : lists) {
            if (head) {
                pq.push(head);
            }
        }
        ListNode dummy{};
        ListNode* head = &dummy;
        while (!pq.empty()) {
            ListNode* node = pq.top();
            pq.pop();
            head->next = node;
            head = head->next;
            if (node->next)
                pq.push(node->next);
        }
        return dummy.next;
    }
};

2️⃣ 分治法

前置题目：21. 合并两个有序链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode dummy{};
        ListNode* cur = &dummy;
        while (list1 && list2) {
            if (list1->val < list2->val) {
                cur->next = list1;
                list1 = list1->next;
            } else {
                cur->next = list2;
                list2 = list2->next;
            }
            cur = cur->next;
        }
        cur->next = list1 ? list1 : list2;
        return dummy.next;
    }

    ListNode* mergeKLists(vector<ListNode*>& lists, int l, int r) {
        if (l == r)
            return lists[l];
        if (l > r)
            return nullptr;
        int m = (l + r) >> 1;
        auto left = mergeKLists(lists, l, m);
        auto right = mergeKLists(lists, m + 1, r);
        return mergeTwoLists(left, right);
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return mergeKLists(lists, 0, lists.size() - 1);
    }
};

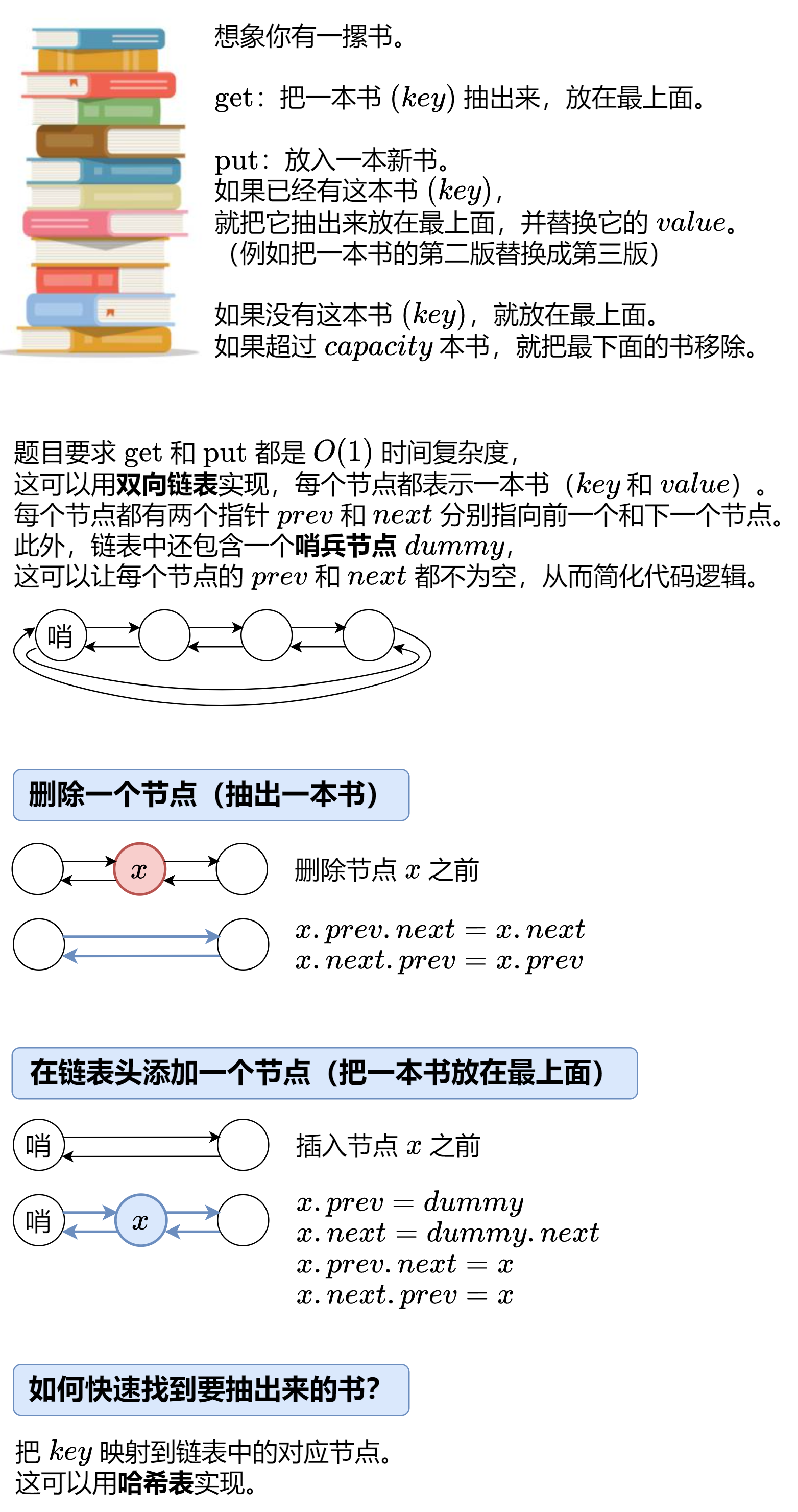
146. LRU 缓存

图解 LRU

struct Node {
    int key;
    int value;
    Node* prev;
    Node* next;
    Node(int k = 0, int v = 0) : key(k), value(v) {}
};

class LRUCache {
private:
    Node* dummy;
    int capacity;
    unordered_map<int, Node*> key_to_node;

    void remove(Node* node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
    }

    void push_front(Node* node) {
        node->next = dummy->next;
        node->prev = dummy;
        dummy->next->prev = node;
        dummy->next = node;
    }

    Node* get_node(int key) {
        if (!key_to_node.count(key)) {
            return nullptr;
        }
        Node* node = key_to_node[key];
        remove(node);
        push_front(node);
        return node;
    }

public:
    LRUCache(int capacity) : capacity(capacity), dummy(new Node()) {
        dummy->next = dummy;
        dummy->prev = dummy;
    }

    int get(int key) {
        Node* node = get_node(key);
        return node == nullptr ? -1 : node->value;
    }

    void put(int key, int value) {
        Node* node = get_node(key);
        if (node != nullptr) {
            node->value = value;
            return;
        }
        node = new Node(key, value);
        if (key_to_node.size() == capacity) {
            Node* last = dummy->prev;
            remove(last);
            key_to_node.erase(last->key);
            delete last;
        }
        key_to_node[key] = node;
        push_front(node);
    }
};

138. 随机链表的复制

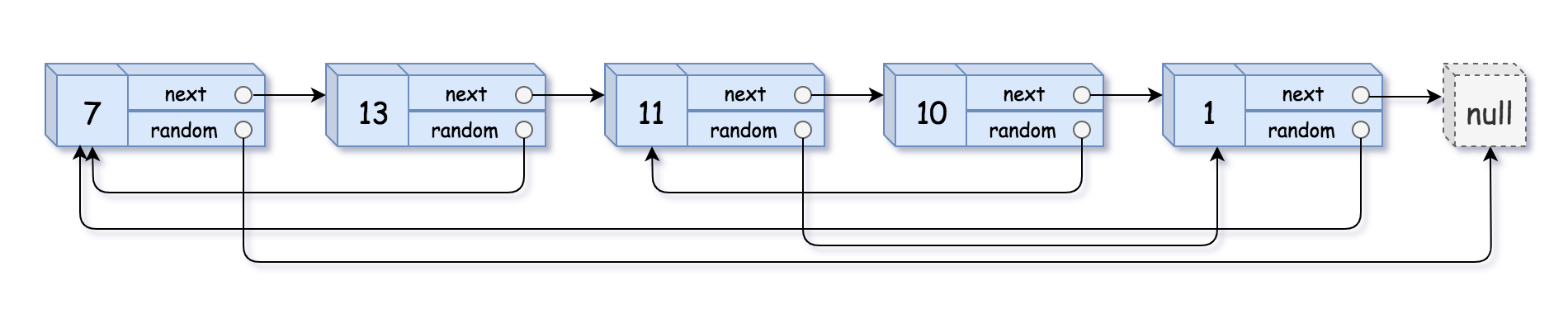
1 2	输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;

    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    unordered_map<Node*, Node*> cacheNode;

    Node* copyRandomList(Node* head) {
        if (head == nullptr)
            return nullptr;
        if (!cacheNode.count(head)) {
            Node* newHead = new Node(head->val);
            cacheNode[head] = newHead;
            newHead->next = copyRandomList(head->next);
            newHead->random = copyRandomList(head->random);
        }
        return cacheNode[head];
    }
};

82. 删除排序链表中的重复元素 II

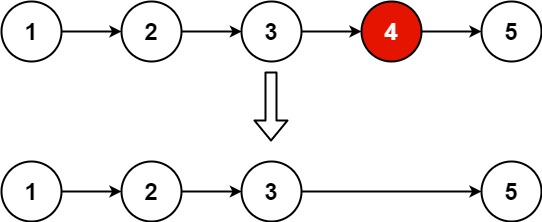
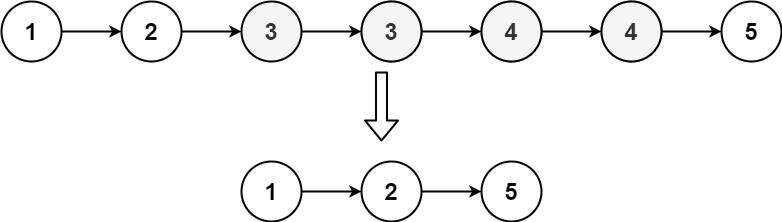
给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        ListNode dummy(0, head);
        auto cur = &dummy;
        while (cur->next && cur->next->next) {
            int val = cur->next->val;
            if (cur->next->next->val == val) {
                while (cur->next && cur->next->val == val) {
                    cur->next = cur->next->next;
                }
            } else {
                cur = cur->next;
            }
        }
        return dummy.next;
    }
};

61. 旋转链表

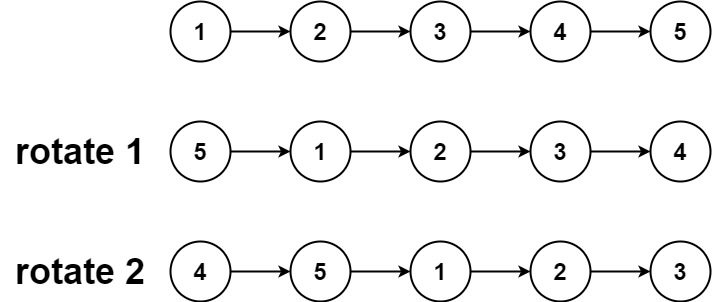
给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

1 2	输入：head = [1,2,3,4,5], k = 2 输出：[4,5,1,2,3]

思路：我们可以先将给定的链表连接成环，然后将指定位置断开。

class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        if (k == 0 || !head || !head->next) {
            return head;
        }
        int n = 1;
        ListNode* iter = head;
        while (iter->next) {
            iter = iter->next;
            n++;
        }
        int t = n - k % n;
        if (t == n)
            return head;
        iter->next = head; // 连成环
        while (t--) {
            iter = iter->next;
        }
        ListNode* ret = iter->next;
        iter->next = nullptr;
        return ret;
    }
};

86. 分隔链表

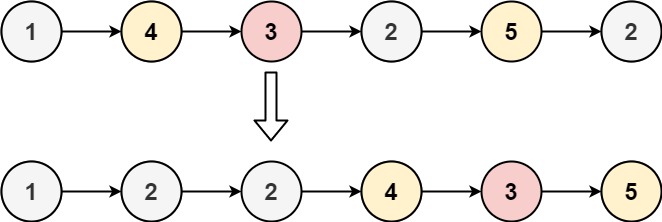
给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当保留两个分区中每个节点的初始相对位置。

1 2	输入：head = [1,4,3,2,5,2], x = 3 输出：[1,2,2,4,3,5]

1️⃣ 模拟

class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        ListNode largeDummy(0);
        ListNode* large = &largeDummy;
        ListNode smallDummy(0);
        ListNode* small = &smallDummy;
        while (head) {
            if (head->val < x) {
                small->next = head;
                small = small->next;
            } else {
                large->next = head;
                large = large->next;
            }
            head = head->next;
        }
        small->next = largeDummy.next;
        large->next = nullptr;
        return smallDummy.next;
    }
};

148. 排序链表

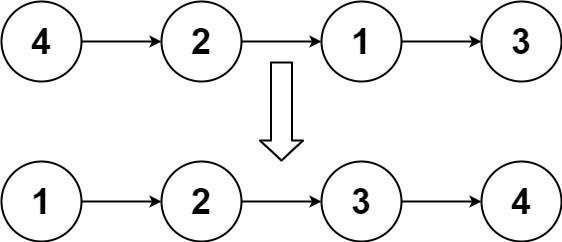
1️⃣ 归并排序（分治法）｜链表的中间结点 + 合并两个有序链表

class Solution {
public:
    // 876. 链表的中间结点（快慢指针）
    ListNode* middleNode(ListNode* head) {
        ListNode* pre = head;
        ListNode* slow = head;
        ListNode* fast = head;
        while (fast && fast->next) {
            pre = slow;
            slow = slow->next;
            fast = fast->next->next;
        }
        pre->next = nullptr; // 断开 slow 与前一个节点的连接
        return slow;
    }

    // 21. 合并两个有序链表 (双指针)
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode dummy;
        ListNode* cur = &dummy;
        while (list1 && list2) {
            if (list1->val < list2->val) {
                cur->next = list1;
                list1 = list1->next;
            } else {
                cur->next = list2;
                list2 = list2->next;
            }
            cur = cur->next;
        }
        cur->next = list1 ? list1 : list2;
        return dummy.next;
    }

    ListNode* sortList(ListNode* head) {
        if (!head || !head->next)
            return head;
        ListNode* mid = middleNode(head);
        ListNode* head1 = sortList(head);
        ListNode* head2 = sortList(mid);
        return mergeTwoLists(head1, head2);
    }
};

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处

高频「链表」面试题

✅ 高频链表面试题

1️⃣ 快慢指针

1️⃣ 快慢指针

1️⃣ 迭代｜三指针

2️⃣ 递归

1️⃣ 快慢指针

1️⃣ 回文链表判断 = 寻找中间节点 + 反转链表

1️⃣ 迭代（常用）

2️⃣ 递归

2. 两数相加 ｜从头开始相加

1️⃣ 迭代

2️⃣ 递归

445. 两数相加 II ｜从尾开始相加

1️⃣ 迭代｜反转链表 + 两数相加

2️⃣ 递归｜反转链表 + 两数相加

1️⃣ 快慢指针

1️⃣ 迭代｜四指针

2️⃣ 递归

1️⃣ 从「反转链表 · 迭代版」到「K 个一组翻转链表」

2️⃣「206. 反转链表」+「92. 反转链表 II」

1️⃣ 最小堆

2️⃣ 分治法

1️⃣ 模拟

1️⃣ 归并排序（分治法）｜链表的中间结点 + 合并两个有序链表

2. 两数相加｜从头开始相加