Maximum product of “subarray” or “subsequence”
字节面试原题⁉️
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续 子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
1
2
3
| 输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
|
1
2
3
| 输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
|
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
vector<long> mx(nums.begin(), nums.end()), mn(nums.begin(), nums.end());
for (int i = 1; i < n; i++) {
mx[i] = max({mx[i - 1] * nums[i], (long)nums[i], mn[i - 1] * nums[i]});
mn[i] = min({mn[i - 1] * nums[i], (long)nums[i], mx[i - 1] * nums[i]});
}
return *max_element(mx.begin(), mx.end());
}
};
|
给你一个下标从 0 开始的整数数组 nums ,它表示一个班级中所有学生在一次考试中的成绩。老师想选出一部分同学组成一个 非空 小组,且这个小组的 实力值 最大,如果这个小组里的学生下标为 i0, i1, i2, … , ik ,那么这个小组的实力值定义为 nums[i0] * nums[i1] * nums[i2] * ... * nums[ik] 。
请你返回老师创建的小组能得到的最大实力值为多少。
1
2
3
| 输入:nums = [3,-1,-5,2,5,-9]
输出:1350
解释:一种构成最大实力值小组的方案是选择下标为 [0,2,3,4,5] 的学生。实力值为 3 * (-5) * 2 * 5 * (-9) = 1350 ,这是可以得到的最大实力值。
|
1
2
3
| 输入:nums = [-4,-5,-4]
输出:20
解释:选择下标为 [0, 1] 的学生。得到的实力值为 20 。我们没法得到更大的实力值。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public:
long long maxStrength(vector<int>& nums) {
long long mn = nums[0], mx = mn;
for (int i = 1; i < nums.size(); i++) {
long long x = nums[i];
long long tmp = mn;
mn = min({mn, x, mn * x, mx * x});
mx = max({mx, x, tmp * x, mx * x});
}
return mx;
}
};
|
给你一个大小为 m x n 的矩阵 grid 。最初,你位于左上角 (0, 0) ,每一步,你可以在矩阵中 向右 或 向下 移动。
在从左上角 (0, 0) 开始到右下角 (m - 1, n - 1) 结束的所有路径中,找出具有 最大非负积 的路径。路径的积是沿路径访问的单元格中所有整数的乘积。
返回 最大非负积 对 10^9 + 7 取余 的结果。如果最大积为 负数 ,则返回 -1 。
注意,取余是在得到最大积之后执行的。
示例 1:

1
2
3
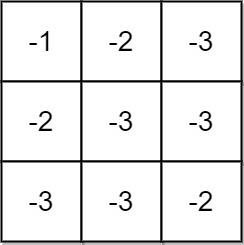
| 输入:grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
输出:-1
解释:从 (0, 0) 到 (2, 2) 的路径中无法得到非负积,所以返回 -1 。
|
示例 2:

1
2
3
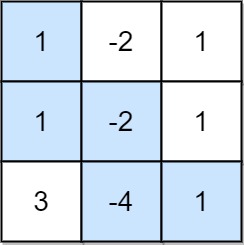
| 输入:grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
输出:8
解释:最大非负积对应的路径如图所示 (1 * 1 * -2 * -4 * 1 = 8)
|
✅ 本题为「鹅厂」与「字节」面试算法题,也是「152. 乘积最大子数组 」的升维算法题
1️⃣ 三维数组
第三维度记录 min 与 max,需要单独初始化第一行和第一列。
由于过程中无法确定最大值的由来,那么需要「左」和「上」的最大最小值来乘于当前值 grid[i][j],与「乘积最大子数组」思路一致。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
int maxProductPath(vector<vector<int>>& grid) {
const int MOD = 1e9 + 7;
int m = grid.size(), n = grid[0].size();
vector f(m, vector(n, vector(2, 0LL)));
f[0][0] = {grid[0][0], grid[0][0]};
for (int j = 1; j < n; j++) {
f[0][j][0] = f[0][j - 1][0] * grid[0][j];
f[0][j][1] = f[0][j - 1][1] * grid[0][j];
}
for (int i = 1; i < m; i++) {
f[i][0][0] = f[i - 1][0][0] * grid[i][0];
f[i][0][1] = f[i - 1][0][1] * grid[i][0];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
int x = grid[i][j];
f[i][j][0] = min({f[i - 1][j][0] * x, f[i - 1][j][1] * x,
f[i][j - 1][0] * x, f[i][j - 1][1] * x});
f[i][j][1] = max({f[i - 1][j][0] * x, f[i - 1][j][1] * x,
f[i][j - 1][0] * x, f[i][j - 1][1] * x});
}
}
return f[m - 1][n - 1][1] >= 0 ? f[m - 1][n - 1][1] % MOD : -1;
}
};
|
2️⃣ 两个二维数组
相当于将方法一三维数组的第三维度拆分成两个二维数组,与「乘积最大子数组」思路一致。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
int maxProductPath(vector<vector<int>>& grid) {
const int MOD = 1e9 + 7;
int m = grid.size(), n = grid[0].size();
vector<vector<long long>> mx(m, vector<long long>(n));
vector<vector<long long>> mn(m, vector<long long>(n));
mx[0][0] = mn[0][0] = grid[0][0];
for (int j = 1; j < n; j++)
mx[0][j] = mn[0][j] = mx[0][j - 1] * grid[0][j];
for (int i = 1; i < m; i++)
mx[i][0] = mn[i][0] = mx[i - 1][0] * grid[i][0];
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
int x = grid[i][j];
mx[i][j] = max({mx[i - 1][j] * x, mn[i - 1][j] * x,
mx[i][j - 1] * x, mn[i][j - 1] * x});
mn[i][j] = min({mx[i - 1][j] * x, mn[i - 1][j] * x,
mx[i][j - 1] * x, mn[i][j - 1] * x});
}
}
return mx[m - 1][n - 1] >= 0 ? mx[m - 1][n - 1] % MOD : -1;
}
};
|