0x3f｜快速幂 - Yikun Wu

qpow

✅ 快速幂

快速幂相关题目：

2961. 双模幂运算 [1451]
2550. 猴子碰撞的方法数 [1663]
372. 超级次方 [算术评级 5]
50. Pow(x, n) [算术评级 5]

1 2	# python 自带快速幂库函数用于计算 x^y mod m pow(x, y, m)

CPP 手撕「快速幂」库函数

// 本题 mod 很小，即使平方也不会超过 int 范围，所以不需要用 long long
int pow(int x, int n, int mod) {
    // long long res
    int res = 1;
    while (n) {
        if (n & 1) {
            res = res * x % mod;
        }
        x = x * x % mod;
        n >>= 1;
    }
    return res;
}

快速幂实现思路（workflow）如下图：

代码实现时，注意 n=−$2^{31}$ 的情况，取反后 n=$2^{31}$ 超出 int 最大值。可以转成 64 位 int 解决（即 long long）

50. Pow(x, n) （包含负数与浮点数）

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，$x^n$ ）。

示例 1：

1 2	输入：x = 2.00000, n = 10 输出：1024.00000

示例 2：

1 2	输入：x = 2.10000, n = 3 输出：9.26100

1️⃣ 快速幂（模板代码）

class Solution {
public:
    double myPow(double x, int N) {
        double ans = 1;
        long long n = N;
        if (n < 0) { // x^-n = (1/x)^n
            n = -n;
            x = 1 / x;
        }
        while (n) { // 从低到高枚举 n 的每个比特位
            if (n & 1) { // 这个比特位是 1
                ans *= x; // 把 x 乘到 ans 中
            }
            x *= x; // x 自身平方
            n >>= 1; // 继续枚举下一个比特位
        }
        return ans;
    }
};

372. 超级次方

你的任务是计算 $a^b$ 对 1337 取模，a 是一个正整数，b 是一个非常大的正整数且会以数组形式给出。

示例 1：

1 2	输入：a = 2, b = [3] 输出：8

示例 2：

1 2	输入：a = 2, b = [1,0] 输出：1024

1️⃣ DFS + 快速幂

class Solution {
public:
    int MOD = 1337;

    int qpow(int x, int n) {
        int res = 1;
        // due to dfs()
        x %= MOD;
        while (n) {
            if (n & 1) {
                res = res * x % MOD;
            }
            x = x * x % MOD;
            n >>= 1;
        }
        return res;
    }

    int dfs(int a, vector<int>& b, int idx) {
        if (idx == -1)
            return 1;
        return qpow(a, b[idx]) * qpow(dfs(a, b, idx - 1), 10) % MOD;
    }

    int superPow(int a, vector<int>& b) {
        return dfs(a, b, b.size() - 1);
    }
};

2550. 猴子碰撞的方法数

现在有一个正凸多边形，其上共有 n 个顶点。顶点按顺时针方向从 0 到 n - 1 依次编号。每个顶点上 正好有一只猴子 。下图中是一个 6 个顶点的凸多边形。

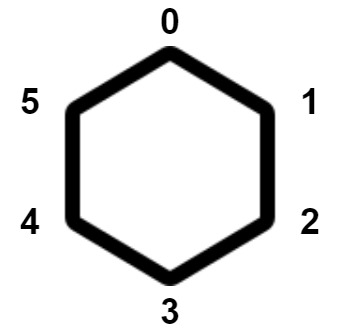
每个猴子同时移动到相邻的顶点。顶点 i 的相邻顶点可以是：

顺时针方向的顶点 (i + 1) % n ，或
逆时针方向的顶点 (i - 1 + n) % n 。

如果移动后至少有两只猴子停留在同一个顶点上或者相交在一条边上，则会发生碰撞。

返回猴子至少发生 一次碰撞 的移动方法数。由于答案可能非常大，请返回对 109+7 取余后的结果。

注意，每只猴子只能移动一次。

示例 1：

输入：n = 3
输出：6
解释：共计 8 种移动方式。
下面列出两种会发生碰撞的方式：
- 猴子 1 顺时针移动；猴子 2 逆时针移动；猴子 3 顺时针移动。猴子 1 和猴子 2 碰撞。
- 猴子 1 逆时针移动；猴子 2 逆时针移动；猴子 3 顺时针移动。猴子 1 和猴子 3 碰撞。
可以证明，有 6 种让猴子碰撞的方法。

1️⃣ 正难则反｜快速幂

只有全部顺时针和全部逆时针这 2 种不会碰撞，所以只需要计算 $2^n-2$，这就需要用到快速幂。

C++：手搓快速幂
Python：使用内置 pow(x, n, mod) 快速幂库函数

class Solution {
public:
    int MOD = 1e9 + 7;

    int qpow(long long x, int n) {
        int res = 1;
        while (n) {
            if (n & 1) {
                res = ((res % MOD) * (x % MOD)) % MOD;
            }
            x = ((x % MOD) * (x % MOD)) % MOD;
            n >>= 1;
        }
        return res;
    }

    int monkeyMove(int n) {
        int ans = qpow(2, n);
        return (ans - 2 + MOD) % MOD;
    }
};

class Solution:
    def monkeyMove(self, n: int) -> int:
        MOD = 1_000_000_007
        return (pow(2, n, MOD) - 2) % MOD

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处