本文不是突发奇想，而是最近刷 LeetCode 曾被灵魂拷问过：“你可以不适用代码库中的排序函数来解决这道题吗？”于是记录并归纳下相关的排序算法～

你可以不使用代码库中的排序函数来解决这道题吗？

🙄不是突发奇想，而是最近刷 LeetCode 曾被灵魂拷问过：“你可以不适用代码库中的排序函数来解决这道题吗？”

转念想想，好像让我随手写个快排都有点棘手，时间偷走了我的记忆，那就用文字记录下叭。

话不多说，本文归纳下各类经典的排序算法。

排序算法🎪

👑因为代码中添加了一些有助于理解的注释，且很多算法都很常见，其排序思想就不再赘述了。

直接插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
public static void insertSort(int[] data) {
    int length = data.length;
    for (int i = 1; i < length; i++) {
        int temp = data[i];
        if (data[i] - data[i - 1] < 0) {
            int j = i - 1;
            for (; j >= 0 && data[j] - temp > 0; j--) {
                data[j + 1] = data[j];
            }
            data[j + 1] = temp;
        }
    }
}

希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static void ShellSort(int[] data) {
    int arrayLength = data.length;
    int h = 1;
    while (h <= arrayLength / 3) {
        h = h * 3 + 1;
    }
    while (h > 0) {
        for (int i = h; i < arrayLength; i++) {
            int temp = data[i];
            if (data[i] - data[i - h] < 0) {
                int j = i - h;
                for (; j >= 0 && data[j] - temp > 0; j -= h) {
                    data[j + h] = data[j];
                }
                data[j + h] = temp;
            }
        }
        h = (h - 1) / 3;
    }
}

简单选择排序

1
2
3
4
5
6
7
8
9
10
11
12
public static void selectSort(int[] data) {
    int arrayLength = data.length;
    for (int i = 0; i < arrayLength - 1; i++) {
        for (int j = i + 1; j < arrayLength; j++) {
            if (data[i] - data[j] > 0) {
                int temp = data[i];
                data[i] = data[j];
                data[j] = temp;
            }
        }
    }
}

堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/**
 * 堆排序
 */
public static void heapSort(int[] data) {
    int arrayLength = data.length;
    // 循环建堆
    for (int i = 0; i < arrayLength - 1; i++) {
        // 建堆
        buildMaxdHeap(data, arrayLength - 1 - i);
        // 交换堆顶和最后一个元素
        swap(data, 0, arrayLength - 1 - i);
    }
}

// 对data数组从0到lastIndex建大顶堆
private static void buildMaxdHeap(int[] data, int lastIndex) {
    // 从lastIndex处节点（最后一个节点）的父节点开始
    for (int i = (lastIndex - 1) / 2; i >= 0; i--) {
        // k保存当前正在判断的节点
        int k = i;
        // 如果当前k节点的子节点存在
        while (k * 2 + 1 <= lastIndex) {
            // k节点的左子节点的索引
            int biggerIndex = 2 * k + 1;
            // 如果biggerIndex小于lastIndex，即biggerIndex +1
            // 代表k节点的右子节点存在
            if (biggerIndex < lastIndex) {
                // 如果右子节点的值较大
                if (data[biggerIndex] - data[biggerIndex + 1] < 0) {
                    // biggerIndex总是记录较大子节点的索引
                    biggerIndex++;
                }
            }
            // 如果k节点的值小于其较大子节点的值
            if (data[k] - data[biggerIndex] < 0) {
                // 交换它们
                swap(data, k, biggerIndex);
                // 将biggerIndex赋给k，开始while循环的下一次循环
                // 重新保证k节点的值大于其左、右节点的值
                k = biggerIndex;
            } else {
                break;
            }
        }
    }
}

// 交换data数组中i、j两个索引处的元素
private static void swap(int[] data, int i, int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

冒泡排序

1
2
3
4
5
6
7
8
9
10
11
public static void bubbleSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * 归并排序
 */
public static void mergeSort(int[] data) {
    sort(data, 0, data.length - 1);
}

// 将索引从left到right范围的数组元素进行归并排序
private static void sort(int[] data, int left, int right) {
    if (left < right) {
        //找出中间索引
        int center = (left + right) / 2;
        sort(data, left, center);
        sort(data, center + 1, right);
        //合并
        merge(data, left, center, right);
    }
}

// 将两个数组进行归并，归并前两个数组已经有序，归并后依然有序
private static void merge(int[] data, int left, int center, int right) {
    int[] tempArr = new int[data.length];
    int mid = center + 1;
    int third = left;
    int temp = left;
    while (left <= center && mid <= right) {
        if (data[left] - data[mid] <= 0) {
            tempArr[third++] = data[left++];
        } else {
            tempArr[third++] = data[mid++];
        }
    }
    while (mid <= right) {
        tempArr[third++] = data[mid++];
    }
    while (left <= center) {
        tempArr[third++] = data[left++];
    }
    while (temp <= right) {
        data[temp] = tempArr[temp++];
    }
}

基数排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static void radixSort(int[] data, int radix, int d) {
    int arrayLength = data.length;
    int[] temp = new int[arrayLength];
    int[] buckets = new int[radix];
    for (int i = 0, rate = 1; i < d; i++) {
        // 重置count数组，开始统计第二个关键字
        Arrays.fill(buckets, 0);
        // 当data数组的元素复制到temp数组中进行缓存
        System.arraycopy(data, 0, temp, 0, arrayLength);
        for (int j = 0; j < arrayLength; j++) {
            int subKey = (temp[j] / rate) % radix;
            buckets[subKey]++;
        }
        for (int j = 1; j < radix; j++) {
            buckets[j] = buckets[j] + buckets[j - 1];
        }
        for (int m = arrayLength - 1; m >= 0; m--) {
            int subKey = (temp[m] / rate) % radix;
            data[--buckets[subKey]] = temp[m];
        }
        rate *= radix;
    }
}

桶排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void BucketSort(int[] data, int min, int max) {
    int arrayLength = data.length;
    int[] temp = new int[arrayLength];
    int[] buckets = new int[max - min];
    
    for (int i = 0; i < arrayLength; i++) {
        buckets[data[i] - min]++;
    }
    
    for (int i = 1; i < max - min; i++) {
        buckets[i] = buckets[i] + buckets[i - 1];
    }
    
    System.arraycopy(data, 0, temp, 0, arrayLength);
    for (int k = arrayLength - 1; k >= 0; k--) {
        data[--buckets[temp[k] - min]] = temp[k];
    }
}

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * 快速排序
 */
public static void quickSort(int[] data) {
    subSort(data, 0, data.length - 1);
}

private static void subSort(int[] data, int start, int end) {
    if (start < end) {
        int base = data[start];
        int low = start;
        int high = end + 1;
        while (true) {
            while (low < end && data[++low] - base <= 0)
                ;
            while (high > start && data[--high] - base >= 0)
                ;
            if (low < high) {
                swap(data, low, high);
            } else {
                break;
            }
        }
        swap(data, start, high);

        subSort(data, start, high - 1);
        subSort(data, high + 1, end);
    }
}

private static void swap(int[] data, int i, int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

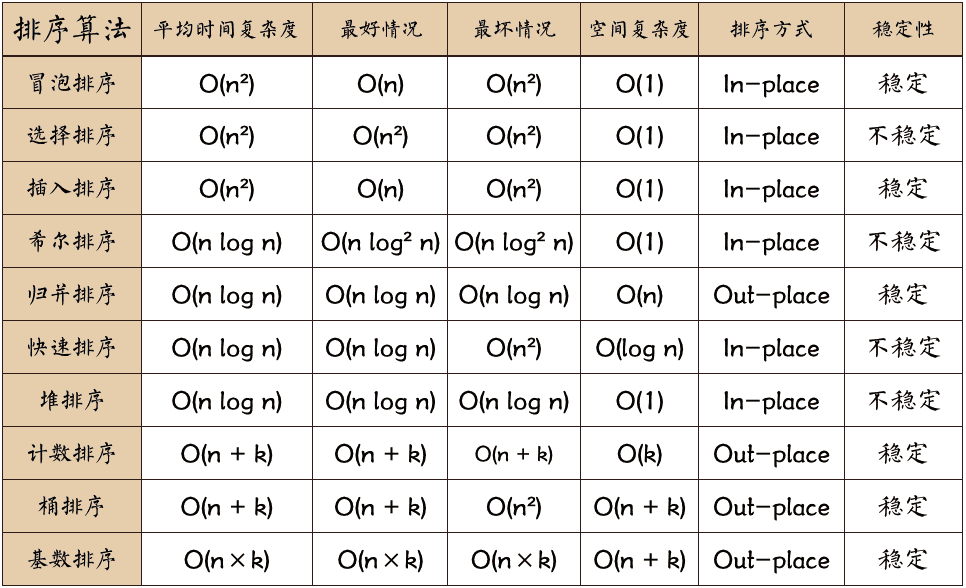
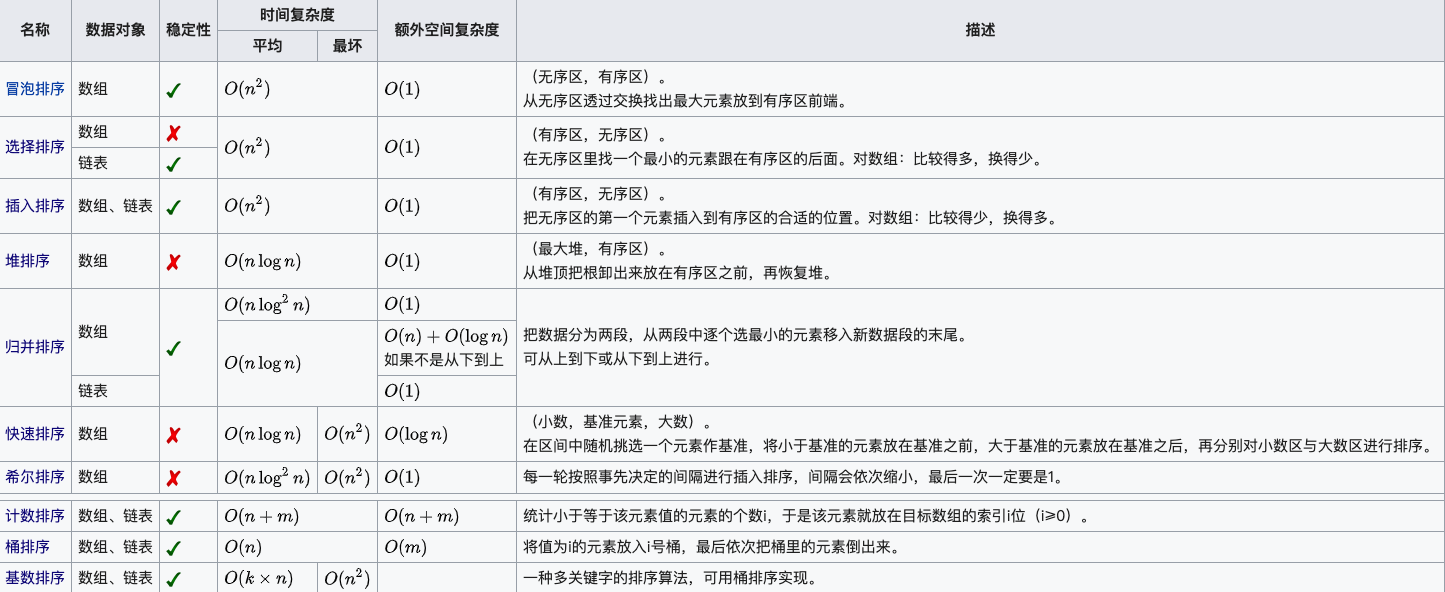
复杂度一览表🍦

图片源于菜鸟教程

😁对于算法的详细分析请参考：十大排序算法

何时调用库函数🔮

不仅是本题的排序算法，LeetCode 中有许多可以调用库函数的地方，那么究竟何时该调用何时别调用呢？

举个栗子：151.翻转字符串里的单词 ，这题本身是综合考察对字符串的处理能力，如果直接调用 split 和 reverse 库函数，那么这道题就失去了它存在的意义。

🚫所以如果题目关键代码可以直接调用库函数解决，建议不要使用库函数，毕竟面试官不是考察你对库函数的熟悉程度。

🔍如果库函数仅是解题过程中的一小部分，并且你已经很清楚这个库函数内部的实现原理的话，可以考虑调用库函数，节省时间。

本着提高代码水平的原则，我想你就会很清楚什么时候该调什么时候不该调了，只有才会有助于对算法的理解。

🌈注意：并非所有语言都像 Python 和 Java 有着丰富的库函数，C、C++ 等语言偏底层，这类所谓的库函数也许得自己手写。

参考资料
许可协议

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处

分享文章
✍️ Yikun Wu 已发表了 69 篇文章 · 总计 293k 字，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处

🌀 本站总访问量 次