2025.05.21 华为笔试题

开发一个简单任务调度系统
地震救灾路线
云计算服务器 GPU 分配

1. 开发一个简单任务调度系统

你需要开发一个简单的任务调度系统，该系统按任务优先级调度，优先级范围是 $(0, 99)$，数值越小优先级越高。只有高优先级任务执行完成后，低优先级任务才能执行，同等优先级的任务按照 $FIFO$ 原则，先进入调度系统的任务会优先调度，当优先级任务执行时，如果新增高优先级任务，高优先级任务会抢占低优先级任务。

请你实现一个程序，模拟这个任务调度系统。

添加任务：将一个新任务添加到任务调度系统。任务包含一个唯一ID（task_id）、优先级（priority）$[0,99]$，运行时间（time）$[1,10000]$。
执行任务：任务调度系统按照调度策略，调度任务并执行。调度系统调度任务，并消耗对应时间片，时间片范围 $[1,100000]$。

Input

程序需要处理以下类型的输入：

添加任务 add task_id priority time
执行任务 run time

注：

输入命令总行数不超过 10000 行
run 命令可以有多个
空行即命令结束

Output

显示任务调度系统当前执行的任务 ID。若无任何任务，则显示 idle。

Sample 1

输入：

add 101 0 10
add 20 1 3
add 300 0 1
run 11

输出：

样例 1 解释：

add 101 0 10：添加任务 101，其优先级为 0，运行时间为 0 个时间片
add 20 1 3：添加任务 20，其优先级为 1，运行时间为 3 个时间片
add 300 0 1：添加任务 30，其优先级为 0，运行时间为 1 个时间片
run 11：调度系统调度任务并执行。首先调度任务 101，运行了 10 个时间片，任务完成。接下来调度任务 300（其优先级高于任务 20），运行了 1 个时间片，任务完成。此时消耗完全部运行时间片（即 11）。
此时调度系统要运行的任务 id 即为 20

Sample 2

输入：

1 2	add 1 0 10 run 11

输出：

idle

样例 2 解释：

add 1 0 10：添加任务 1，优先级 0，运行时间为 10 个时间片
run 11：调度系统调度任务，并运行 11 个时间片。选择任务 1 运行了 10 个时间片，任务 1 完成。无任务待调度。
调度系统无任何任务，因此显示 idle。

Solution (False)

每执行一次 run 则输出一次结果

#include <bits/stdc++.h>
using namespace std;

struct Task {
    int id;
    int priority;
    int remain;  // 剩余时间片
};

// 每个优先级维护一个FIFO队列, 下标0是最高优先级
queue<Task> slots[100];

// 添加任务
void addTask(int id, int priority, int time) {
    slots[priority].push({id, priority, time});
}

// 获取下一个待执行任务, 如果无任务则返回{-1,-1,-1}
Task getNext() {
    for (int p = 0; p < 100; ++p) {
        if (!slots[p].empty()) {
            Task t = slots[p].front();
            slots[p].pop();
            return t;
        }
    }
    return {-1, -1, -1};
}

int getCurrentTaskId() {
    for (int p = 0; p < 100; ++p) {
        if (!slots[p].empty()) {
            return slots[p].front().id;
        }
    }
    return -1;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    string cmd;
    while (getline(cin, cmd)) {
        if (cmd.empty()) break;
        stringstream ss(cmd);
        ss >> cmd;
        if (cmd == "add") {
            int id, pr, t;
            ss >> id >> pr >> t;
            addTask(id, pr, t);
        } else if (cmd == "run") {
            int time;
            ss >> time;
            while (time > 0) {
                Task cur = getNext();
                if (cur.id == -1) break;  // 无任务
                if (cur.remain <= time) {
                    time -= cur.remain;  // 任务完成, 消耗所有剩余时间
                } else {
                    cur.remain -= time;  // 任务未完成
                    time = 0;
                    slots[cur.priority].push(cur);  // 重新排队
                }
            }
            int nid = getCurrentTaskId();
            if (nid == -1) cout << "idle";
            else cout << nid;
            cout << "\n";
        }
    }
    return 0;
}

Solution (True)

只输出最后一次 run

✅ 参考链接：https://codefun2000.com/p/P2972

#include <bits/stdc++.h>
using namespace std;

// 任务结构体
struct Task {
    int id;     // 任务ID
    int prio;   // 优先级（越小越先）
    int rem;    // 剩余时间片
    int order;  // 到达顺序
};

// 优先队列比较器
struct Cmp {
    bool operator()(const Task &a, const Task &b) const {
        if (a.prio != b.prio) return a.prio > b.prio;
        return a.order > b.order;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    priority_queue<Task, vector<Task>, Cmp> pq;
    string cmd;
    int next_order = 0;
    vector<pair<string, vector<int>>> ops;

    // 读取所有操作
    while (getline(cin, cmd)) {
        if (cmd.empty()) break;
        stringstream ss(cmd);
        string op; ss >> op;
        if (op == "add") {
            int id, p, t; ss >> id >> p >> t;
            ops.push_back({op, {id, p, t}});
        } else if (op == "run") {
            int T; ss >> T;
            ops.push_back({op, {T}});
        }
    }

    // 模拟所有操作，只在最后一次 run 后输出
    int last_run_idx = -1;
    for (int i = 0; i < (int)ops.size(); i++) {
        if (ops[i].first == "run") last_run_idx = i;
    }

    for (int i = 0; i < (int)ops.size(); i++) {
        auto &op = ops[i];
        if (op.first == "add") {
            // 入队一个新任务
            pq.push({op.second[0], op.second[1], op.second[2], next_order++});
        } else {
            int T = op.second[0];
            while (T > 0 && !pq.empty()) {
                Task t = pq.top(); pq.pop();
                if (t.rem <= T) {
                    T -= t.rem;  // 任务完成，消耗全部剩余时间
                } else {
                    t.rem -= T;  // 任务未完成，更新剩余时间
                    T = 0;
                    pq.push(t);  // 重新入队
                }
            }
            // 如果是最后一次 run，输出结果
            if (i == last_run_idx) {
                if (pq.empty()) cout << "idle\n";
                else cout << pq.top().id << "\n";
            }
        }
    }
    return 0;
}

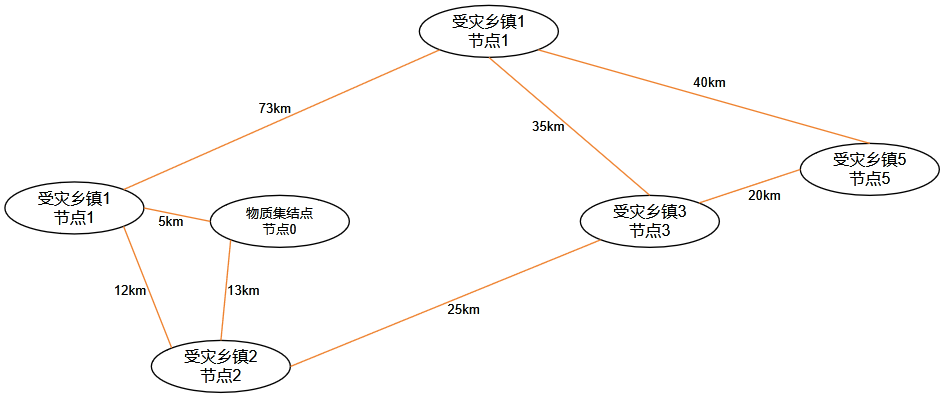
2. 地震救灾路线

某市发生地震，为了尽快将救援物质输送到受灾乡镇，需要你设计出从救援物质集结点（有仅有一个）到某一个受灾乡镇的最短线路

应急部门通过无人机助察了受灾地区地形，提供了各乡镇之间以及乡镇到救援物质集结点的距离，请你算出救援物质集结点到受灾多镇的最短路径。

Input

第一行，N，受灾乡镇个数，3<=N<=20

第二行至第 N+2 行，救援物质集结点以及各乡镇之间的距离矩阵（即 N+1 个节点之间的相互距离矩阵），距离取值范围是 $[0,100]$。序号 0 的节点表示救援物质集结点，序号 1 ~ N 的节点表示各个受灾乡镇。0 表示两个节点不相邻。

第 N+3 行，m，要抵达的乡镇序号（范围 1~N）

Output

从物质集结点（节点 0）到乡镇 m（节点 m）的最短路径长度

Sample 1

输入：

5
0 5 13 0 0 0
5 0 12 0 75 0
13 12 0 25 0 0
0 0 25 0 35 20
0 75 0 35 0 40
0 0 0 20 40 0
3

输出：

样例 1 解释：

从 0 到 3 的最短路径为 $0-2-3$，长度为 $13 + 25 = 38$

Sample 2

输入：

5
0 5 13 0 0 0
5 0 12 0 75 0
13 12 0 25 0 0
0 0 25 0 35 20
0 75 0 35 0 40
0 0 0 20 40 0
5

输出：

样例 2 解释：

从 0 到 5 的最短路径为 $0-2-3-5$，长度为 $13+25+20=58$

Solution

✅ 参考链接：https://codefun2000.com/p/P2973

#include <bits/stdc++.h>
using namespace std;

int main() {
    int N;
    cin >> N; // 受灾乡镇个数
    int total = N + 1;
    vector<vector<int>> d(total, vector<int>(total));
    // 读入距离矩阵，节点 0 为物资集结点，1~N 为乡镇
    for (int i = 0; i < total; i++) {
        for (int j = 0; j < total; j++) {
            cin >> d[i][j];
        }
    }
    int m;
    cin >> m; // 目标乡镇编号

    const int INF = 1e9;
    vector<int> dist(total, INF);
    vector<bool> vis(total, false);

    dist[0] = 0; // 源点到自己的距离为 0

    // Dijkstra 算法主循环
    for (int i = 0; i < total; i++) {
        int u = -1, minDist = INF;
        // 找到未访问且 dist 最小的节点 u
        for (int j = 0; j < total; j++) {
            if (!vis[j] && dist[j] < minDist) {
                u = j;
                minDist = dist[j];
            }
        }
        if (u == -1) break; // 剩余节点不可达
        vis[u] = true;
        // 松弛以 u 为起点的所有边
        for (int v = 0; v < total; v++) {
            if (!vis[v] && d[u][v] > 0 && dist[v] > dist[u] + d[u][v]) {
                dist[v] = dist[u] + d[u][v];
            }
        }
    }

    cout << dist[m] << endl; // 输出从 0 到 m 的最短距离
    return 0;
}

补充｜Dijkstra 算法

Dijkstra 算法是一种求解非负权图上单源最短路径的算法。

算法思路‼️

将结点分成两个集合：已确定最短路长度的点集（记为 $S$ 集合）的和未确定最短路长度的点集（记为 $T$ 集合）。一开始所有的点都属于 $T$ 集合。

初始化 $dis(s) = 0$，其他点的 $dis$ 均为 $+∞$。

然后重复这些操作：

从 $T$ 集合中，选取一个最短路长度最小的结点，移到 $S$ 集合中。
对那些刚刚被加入 $S$ 集合的结点的所有出边执行松弛操作。

直到 $T$ 集合为空，算法结束。

时间复杂度

朴素的实现方法为每次「操作 2」执行完毕后，直接在 $T$ 集合中暴力寻找最短路长度最小的节点。「操作 2」总时间复杂度为 $O(m)$，「操作 1」总时间复杂度为 $O(n^2)$，全过程的时间复杂度为 $O(n^2+m)=O(n^2)$。

可以用「堆」来优化这一过程：每松弛一条边 $(u,v)$，就将 $v$ 插入堆中（如果 $v$ 已经在堆中，直接执行 Decrease-key），「操作 1」直接取堆顶节点即可。共计 $O(m)$ 次 Decrease-key，$O(n)$ 次 pop，堆优化能做到的最优复杂度为 $O(nlogn+m)$。特别地，可以用优先队列 priority_queue 维护，此时无法执行 Decrease-key 操作，但可以通过每次松弛时重新插入该节点，且弹出时检查该节点是否已被松弛过，若是则跳过，复杂度 $O(mlogn)$，优点是实现比较简单。

这里的堆也可以用线段树实现，复杂度为 $O(mlogn)$，在一些特殊的非递归线段树实现下，该做法常数比堆更小。并且线段树支持的操作更多，在一些特殊图问题上只能用线段树来维护。

✅ 在稀疏图（邻接矩阵）中，$m=O(n)$，堆优化的 Dijkstra 算法具有较大的效率优势；

✅ 而在稠密图（邻接图）中，$m=O(n^2)$，这时候使用朴素实现更优。

代码实现

这里同时给出 $O(n^2)$ 的暴力做法实现和 $O(m·logm)$ 的优先队列做法实现。

dijkstra 算法推荐练习题：

1️⃣ 朴素实现｜稠密图（邻接图）

struct edge {
  int v, w;
};

vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];

void dijkstra(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  dis[s] = 0;
  for (int i = 1; i <= n; i++) {
    int u = 0, mind = 0x3f3f3f3f;
    for (int j = 1; j <= n; j++)
      if (!vis[j] && dis[j] < mind) u = j, mind = dis[j];
    vis[u] = true;
    for (auto ed : e[u]) {
      int v = ed.v, w = ed.w;
      if (dis[v] > dis[u] + w) dis[v] = dis[u] + w;
    }
  }
}

2️⃣ 优先队列实现｜稀疏图（邻接矩阵）

struct edge {
  int v, w;
};

struct node {
  int dis, u;

  bool operator>(const node& a) const { return dis > a.dis; }
};

vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];
priority_queue<node, vector<node>, greater<node>> q;

void dijkstra(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  memset(vis, 0, (n + 1) * sizeof(int));
  dis[s] = 0;
  q.push({0, s});
  while (!q.empty()) {
    int u = q.top().u;
    q.pop();
    if (vis[u]) continue;
    vis[u] = 1;
    for (auto ed : e[u]) {
      int v = ed.v, w = ed.w;
      if (dis[v] > dis[u] + w) {
        dis[v] = dis[u] + w;
        q.push({dis[v], v});
      }
    }
  }
}

3. 云计算服务器 GPU 分配

某云计算服务商为客户提供 M 数量 GPU 核数的 GPU 分时租用服务，租用计费规则为：允许客户在每个时间单位按需租用不同的 GPU 核数，每个时间单位每个 GPU 核数的费用为 R。现有 N 个客户，每个客户有多个不重叠时间租用一定数量的 GPU 核数租用需求。对于有需求的客户，服务商可选择签约或不签约，若选择签约则需要满足租用需求中的所有时间段所需的 GPU 核数。

为了实现租金最大化收益，服务商需在确保任意时间单位内分配的 GPU 核数总数不超过 M 的基础上选择与哪些客户签约租用协议。

请输出租金最大化收益下的租金最大值。

Input

第一行为 M、N、R 的数值，依次用空格隔开，输入格式为 M N R。

从第二行开始，每行为一个客户的租用需求，共 N 行。每行的第一个数字为该客户端的时间段个数 timeSegmentNum，后续为 timeSegmentNum 个时间段及所需的 GPU 核数，时间段个数 timeSegmentNum 与时间段之间、多个时间段之间均用空格分割，同一个客户多个时间段已按起始时间增序排序给出。同个客户多个时间段不会重叠。同一个客户多个时间段已按起始时间增序排序给出。

每个时间段及所需的 GPU 核数格式为 start 起始时间编号:end 结束时间编号:needcores 该时间段所需的 GPU 核数。

变量取值范围

$1<=M<=100000$
$1<=N<=10$
$1<=R<=10$
$0<= start<= end<= 10^9$
$0<= start<= end<= 10^9$
$1<= needCores<= 10000$
$1<= timeSegmentNum <= 100$

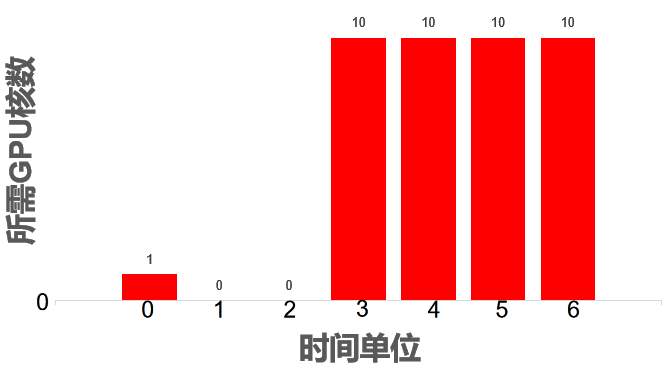
客户的租用需求样例 $2$、$0:0:1$、$3:6:10$ 的含义是共有 2 个时间段，0:0:1 表示在第 0 个时间单位需要 1 个 GPU 核，3:6:10 表示从 3 到 6 的时间单位（包含 3 和 6）每个时间单位均需 10 个 GPU 核。

图例为：

Output

总租金最大值。如果任意一个客户的需求都无法满足，则输出 0

Sample 1

输入：

10 3 2
2 0:8:5 9:23:10
2 0:8:5 9:18:10
1 0:8:5

输出：

样例 1 解释：

共 3 个客户。

由于第一个客户和第二个客户在 $9:18$ 时间范围段内总核数为 20 超过了 10，所以无法同时接受。

最大日租金方案为：接纳第一个客户和第三个客户的需求。

第一个客户共需要的GPU核数为 $9 * 5 + 15*10=195$

第三个客户共需要的GPU核数为 $9 * 5=45$

Sample 2

输入：

1
2
3

10 2 1
1 0:3:6
1 3:10:6

输出：

样例 2 解释：

最大 GPU 核数为 10，共 2 个客户。

第一客户和第二个客户在3时间点，总核数为 12 超过了 10，所以无法同时接受。

第一个客户共需要的GPU核数为 $4 * 6=24$

第二个客户共需要的GPU核数为 $8 * 6=48$

为满足最大租金，采纳第二个客户，最大租金值为（48）* 1=48

Sample 3

输入：

1 2	10 1 1 1 0:5:20

输出：

样例 3 解释：

最大 GPU 核数为 10，共 1 个客户。
在 $0-5$ 时间段需要 20 个 GPU 核数，无法满足。

Sample 4

输入：

1 2	10000 1 10 1 0:1000000000:10000

输出：

1	1000000000100000

样例 4 解释：

最大 GPU 核数为 10000，共 1 个客户。

客户在 $0-100000000$ 时间段需要 10000 个GPU核数，可以满足。

租金最大值为 1000000000100000

Solution

✅ 参考链接：https://codefun2000.com/p/P2974

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    // 读入 M, N, R
    ll M; int N; ll R;
    cin >> M >> N >> R;

    // 存储每个客户的时间段需求
    vector<vector<tuple<ll,ll,ll>>> segs(N);
    for (int i = 0; i < N; i++) {
        int t; cin >> t;
        while (t--) {
            ll s, e, c;
            char ch;
            cin >> s >> ch >> e >> ch >> c;  // 读入格式 s:e:c
            segs[i].emplace_back(s, e, c);
        }
    }

    ll ans = 0;
    // 枚举所有子集
    for (int mask = 0; mask < (1<<N); mask++) {
        vector<ll> xs;
        ll W = 0;
        // 收集边界
        for (int i = 0; i < N; i++) if (mask & (1<<i)) {
            for (auto &seg: segs[i]) {
                ll s,e,c; tie(s,e,c) = seg;
                xs.push_back(s);
                xs.push_back(e+1);
                W += (e - s + 1) * c;
            }
        }
        if (xs.empty()) continue;
        // 离散化
        sort(xs.begin(), xs.end());
        xs.erase(unique(xs.begin(), xs.end()), xs.end());
        vector<ll> diff(xs.size()+1);
        // 差分数组构造
        for (int i = 0; i < N; i++) if (mask & (1<<i)) {
            for (auto &seg: segs[i]) {
                ll s,e,c; tie(s,e,c) = seg;
                int l = lower_bound(xs.begin(), xs.end(), s) - xs.begin();
                int r = lower_bound(xs.begin(), xs.end(), e+1) - xs.begin();
                diff[l] += c;
                diff[r] -= c;
            }
        }
        // 扫描检查容量
        ll cur = 0;
        bool ok = true;
        for (int i = 0; i+1 < (int)xs.size(); i++) {
            cur += diff[i];
            if (cur > M) { ok = false; break; }
        }
        if (ok) ans = max(ans, W * R);
    }

    cout << ans;
    return 0;
}

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。